Calcule o módulo da força suportada pelo pino em no dispositivo em curva, carregado e apoiado como mostrado.
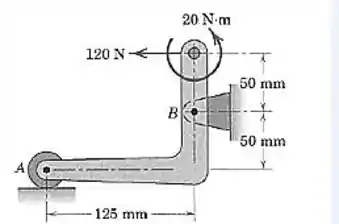
Passo 1
Aqui vamos ter que atender a três condições:
Passo 2
A forças de reação em e tem uma forma dada por:
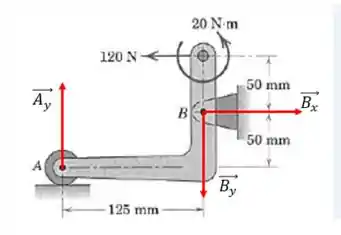
Perceba que a componente da reação em é nula. Isso se deve ao fato de que o apoio em é um apoio deslizante, ou seja, não há o impedimento desse apoio de se mover na horizontal. E não se esqueça: só colocamos reação de apoio na direção onde há impedimento do movimento.
Sendo assim, já descobrimos quanto vale
Passo 3
Agora vamos fazer o seguinte: calcular o equilíbrio de momentos em relação ao ponto
Vamos considerar o sentido anti-horário como o positivo:
Não pode esquecer de contabilizar o momento de que já tinha na estrutura.
Então, obtemos o seguinte:
Passo 4
Agora, usando o somatório de forças verticais:
Passo 5
Sendo assim, o módulo de será: