02) A estrutura da figura, composta pelas barras articuladas e , todas de peso desprezível, está em equilíbrio sob a ação do carregamento indicado. Pede-se:
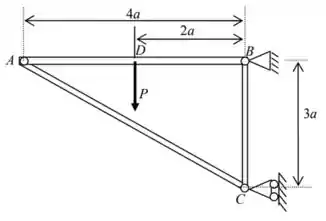
a) Determinar as reações vinculares;
b) Construir os diagramas de corpo livre das barras;
c) Determinar as forças internas nas barras e .
Passo 1
Faaala galera, tudo tranquilo com vocês?
a) Nessa questão temos uma estrutura composta por barras. Pra começar precisamos determinar as reações nos apoios e . Como podemos fazer isso?

Antes de tudo é uma boa nós desenharmos um diagrama de corpo livre da estrutura inteira, considerando só as forças externas, sabem?
Pela figura, o apoio em é do gênero, assim só a reação em um eixo. Já o apoio em é do gênero, e possui reação de apoio em dois eixos.
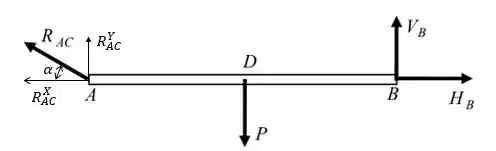
Além dos apoios há também uma força atuando no ponto da estrutura. Daí, considerando o eixo vertical como e o horizontal como , podemos desenhar o seguinte DCL:
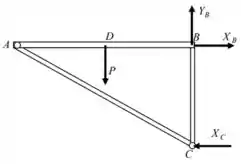
Como a estrutura está em equilíbrio, podemos montar as seguintes equações:
De , vem:
De vem:
De vem:
Logo:
Prontinho 😊
Determinamos as reações vinculares!
Passo 2
b) Nesse item precisamos desenhar os diagramas de corpo livre das barras. Bora olhar novamente a figura da estrutura:
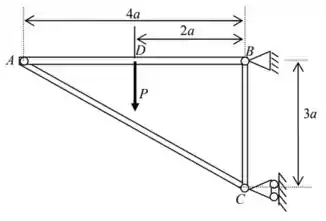
Começando pela barra , vemos que em e ela é rotulada. Por isso, funciona tipo as barras de treliça, com força de tração ou compressão. Vamos supor que inicialmente esteja comprimida:

Analisando agora a barra vai ser bem parecido, as forças se concentram nos seus nós e , de modo que é como uma barra de treliça, cuja força interna está ao longo do seu eixo. Vamos supor que seja também de compressão:
![]()
Para finalizar, vamos observar a barra . Ela é um pouco diferente, pois possui uma carga no meio dela. Por isso, não dá pra considerar como se fosse uma simples barra de treliça com força interna ao longo de seu eixo.
O melhor é analisar a contribuição de cada nó com a lei da “ação e reação” em mente. No nó A, deve haver uma força contrária a . No nó temos a contribuição tanto na vertical como na horizontal, , atuando.
Assim:
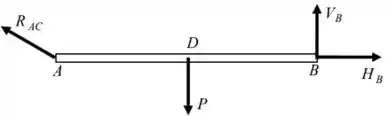
Prontinho! Mais um item finalizado 😉
Passo 3
c) Para matar de vez essa questão, nesse item devemos calcular as forças internas nas barras.
A ideia pra conseguir calcular essas reações é escrever as equações de equilíbrio. Bora começar escrevendo para a barra .
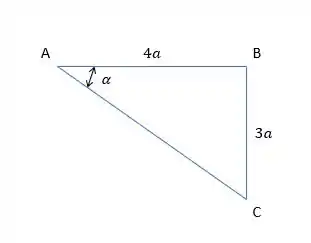
Antes disso, pela geometria da figura, também podemos desenhar:
Logo:
Massa! Agora vamos pras equações:
Temos:
Daí:
Show! Usando as outras equações do equilíbrio, temos:
Só nos falta descobrir o valor de . Analisando o equilíbrio de forças no nó , temos:
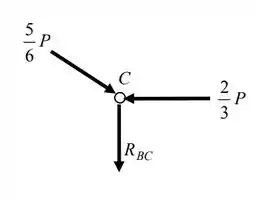
Para que ele esteja em equilíbrio, devemos ter . Logo:
Ufaa! Acabamos! O sinal negativo significa apenas que os sentidos supostos inicialmente estão invertidos 😉
É isso galera, até a próxima!
Resposta
a)
b) Resolução no texto.
c) Resolução no texto.