O conector de correntes é utilizado para segurar cargas de troncos, madeira, tubos e congêneres. Se a força trativa vale quando , determine a força necessária na alavanca e a força trativa correspondente para essa posição. Admita que a superfície sob é perfeitamente lisa.
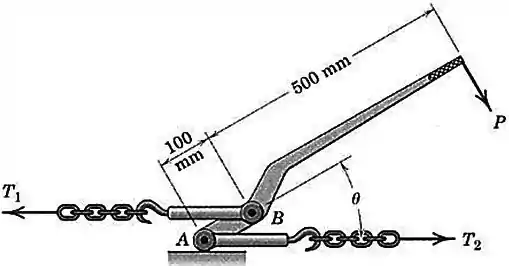
Passo 1
O diagrama de corpo livre fica assim:
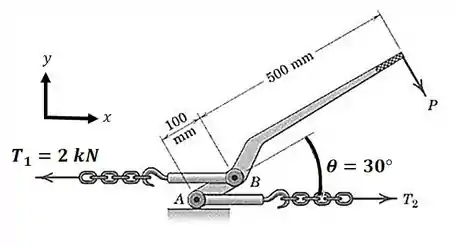
Passo 2
Repare que pelo ponto passa a linha de ação da força trativa , então essa força não exerce momento neste ponto.
Então, vamos começar calculando o momento com relação ao ponto para podermos achar o valor de :
Mas antes vamos achar as distâncias das forças até o ponto .
Passo 3
Vamos começar achando a distância da força com relação ao ponto . Mas repare que a força está inclinada... Então, temos que achar a distância de cada uma de suas componentes com relação ao ponto .
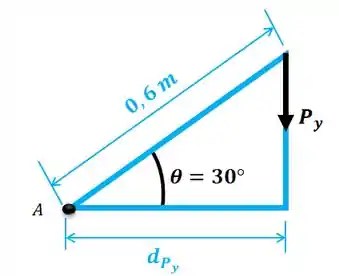
Temos que a distância é:
E para a componente , temos:
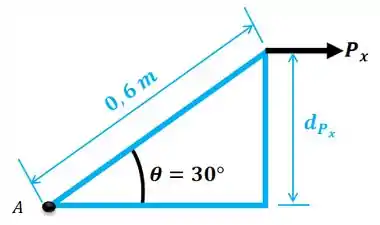
Passo 4
Agora vamos achar a distância da força com relação ao ponto . Para isso, vamos usar este triângulo aqui:
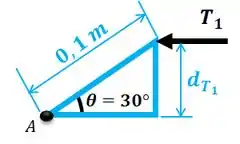
Passo 5
Agora vamos decompor a força :
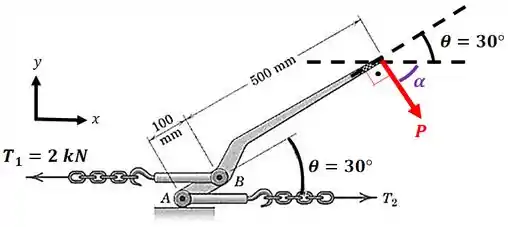
Vamos achar o ângulo que a força faz com relação a horizontal. Repare que a soma dos ângulos deve dar , então:
Agora sim podemos achar as componentes da força :
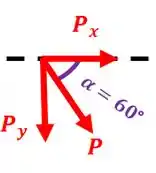
Então:
E:
Passo 6
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passando isso para Newton, temos:
Passo 7
Agora vamos fazer o somatório de forças horizontais:
Repare que estamos usando todas as forças na mesma unidade que é Newton!
Então: