Determine a força necessária para começar a rolar o cilindro uniforme de massa sobre o degrau
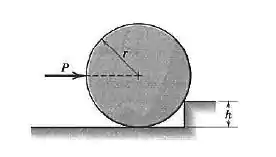
Passo 1
Bom, a primeira coisa que precisamos fazer é determinar quais são as forças que atuam no cilindro. São essas:
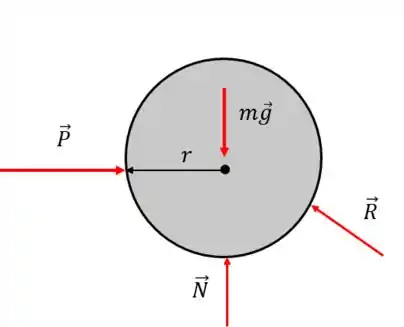
A força , que empurra o cilindro. A normal , devido ao contato do cilindro com o chão. E a reação , devido ao contato do cilindro com o degrau.
Passo 2
Beleza, mas nós queremos a força necessária para o cilindro subir. Isso quer dizer, em outras palavras, que a normal com o chão é nula: na iminência do giro, o cilindro perde o contato com o chão:
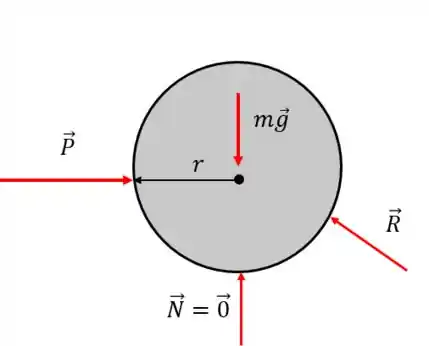
Bom, essa informação não vai ser tão relevante para achar o valor de , pelo menos não através do caminho que usaremos. Mas fica aí a informação teórica sobre isso.
Observação: estamos, é claro, procurando o valor do módulo de .
Passo 3
Bom, preste atenção no triângulo abaixo. Ele é formado pelas distâncias dadas na questão:
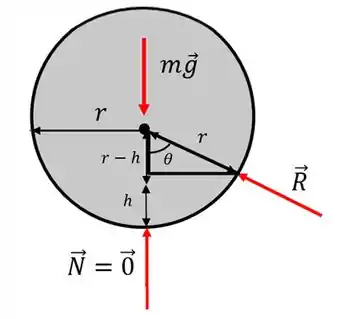
Vamos tirar este triângulo de dentro do outro desenho para facilitar a nossa visualização:
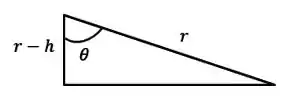
Passo 4
Vamos calcular o cosseno do ângulo que aparece no triângulo. Você entenderá nos próximos passos, quando formos decompor a força peso no cálculo do momento:
E, usando:
Sabemos que:
Então, vamos substituir isso na outra equação:
Desenvolvendo, chegamos a:
Passo 5
Agora vem o pulo do gato: vamos usar o equilíbrio de momentos para calcular o valor de
Na iminência de girar, o momento causado pela força compensa os momentos das outras forças.
Tomando o ponto de contato do cilindro com o degrau como referência, teremos as seguintes forças exercendo o momento: o peso e a força
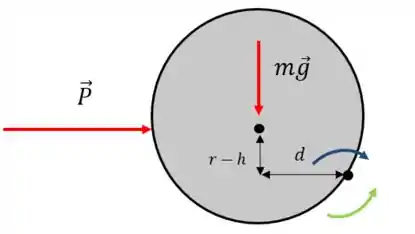
Assim:
Sacou?
Bom, e quanto vale
Passo 6
Agora sim vamos usar o nosso triângulo:
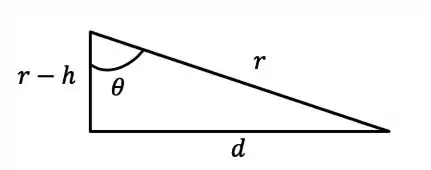
Sacou? é dado por:
E quanto vale
Assim:
Assim, voltando ao cálculo dos momentos:
Pronto!