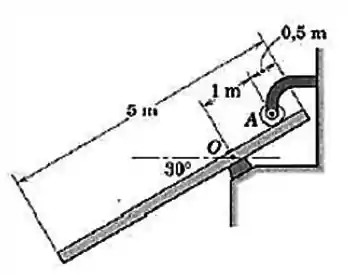
A barra uniforme de e massa de é articulada em e impedida de girar mais do que no plano vertical pelo rolete fixo em . Calcule o módulo da força total suportada pelo pino em .
Passo 1
O diagrama de corpo livre pode ser representado por:
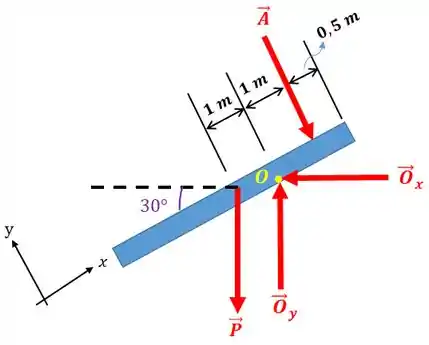
Passo 2
O módulo da força peso da barra vale:
Agora vamos decompor esta força no eixo :
Agora vamos usar o equilíbrio de momentos em relação ao ponto e considerando o sentido de giro anti-horário como positivo, temos:
Passo 3
Usando o equilíbrio de forças horizontais:
E o vertical:
Então, a resultante de forças no ponto é: