Determine a força necessária para manter o motor de na posição para a qual . O diâmetro em é desprezível.
Passo 1
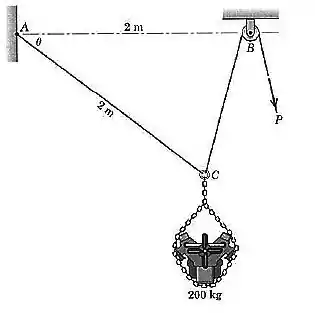
Se você reparar bem vai ver que esse é o caso em que as forças são concorrentes em um ponto só, ou seja, a linha de ação das forças passa por um dos ponto do desenho?
Você consegue identificar este ponto? É o ponto , dê uma olhadinha aqui:
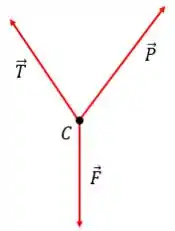
Esse é o nosso diagrama de corpo livre.
Perceba que, por se tratar de uma corda, a força pode ser representada ao longo de toda esta corda. Então, o que fizemos aqui foi transmitir a força e representá-la na direção .
Passo 2
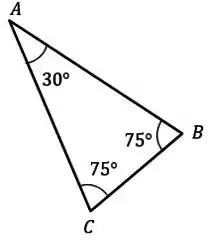
Vamos usar um pouquinho de geometria agora: Perceba que esse é um triângulo que possui dois lados iguais. Assim, ele terá também dois ângulos iguais.
Perceba também que um dos três ângulos do triângulo vale . Sabendo que a soma dos ângulos dá , podemos escrever assim:
Assim:
Passo 3
Então, colocando esses ângulos no nosso diagrama de corpo livre, temos isso aqui:
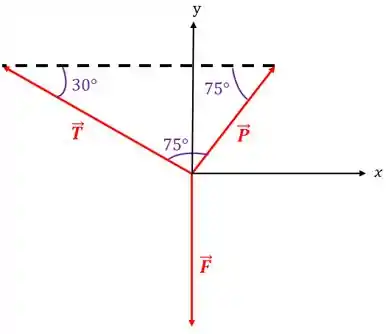
Agora, temos que decompor todas as forças nos eixos e para podermos fazer as somas dos vetores. Mas repare que temos que descobrir mais alguns ângulos para poder decompor esses vetores:
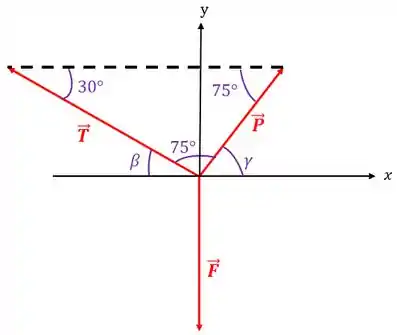
Repare que somando os ângulos e com obtemos :
Mas... Como vamos resolver essa equação se ela tem duas incógnitas? Temos que achar mais um ângulo antes. Para isso, vamos usar este triângulo aqui:
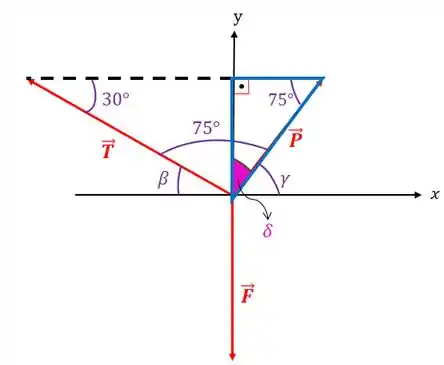
Vamos isolar esse triângulo que queremos para entendermos melhor o que precisamos fazer:
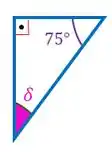
A soma de todos os ângulos internos de um triângulo deve dar , então:
Passo 4
Agora já conseguimos achar o ângulo :
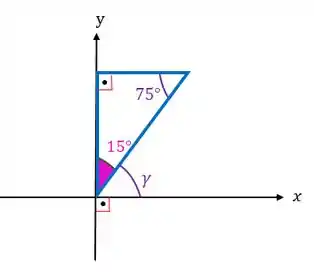
Repare que os eixos e são perpendiculares entre si, então:
Beleza?
Agora vamos resgatar aquela equação que não conseguimos resolver:
Passo 5
Pronto! Achamos todos os ângulos que eram necessários:
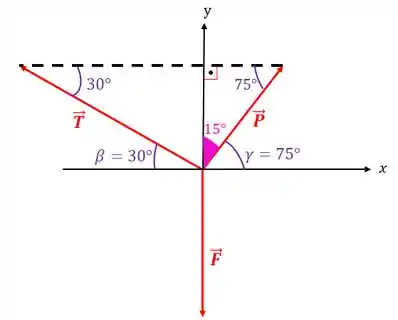
Então, vamos calcular o valor do módulo da força que é nada mais nada menos que o peso do motor:
Escrevendo esta força como um vetor, temos:
Agora vamos decompor a força e a força nos eixos e :
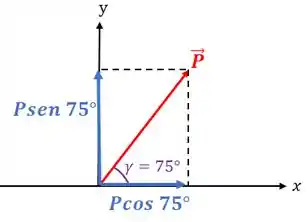
E a força fica assim:
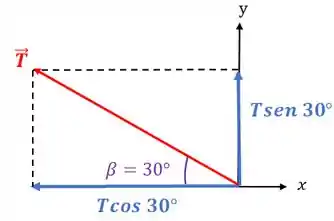
Passo 6
Vamos fazer agora o equilíbrio destas forças. Sabemos que a soma de todas as forças horizontais deve ser zero, então:
Vamos isolar a força para substituir na próxima equação:
Beleza?
Agora vamos fazer o equilíbrio das forças verticais:
Vamos substituir pela equação que achamos ali em cima:
Substituindo todos os valores de senos e cossenos, vamos ter que: