Considere a curva de energia potencial, figura 2, , entre duas partículas e , onde é a distância entre elas. Marque a alternativa incorreta:
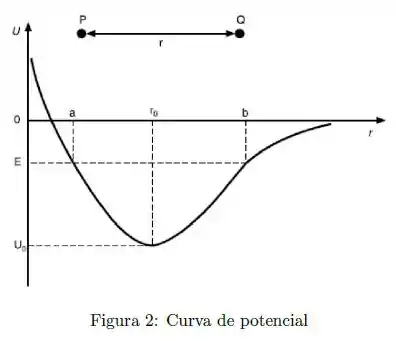
(A) O ponto de equilíbrio vale .
(B) O ponto de equilíbrio é estável.
(C) Se a energia mecânica total for igual a , a distância das partículas oscila em torno de .
(D) Se a energia mecânica total for igual a , existem dois pontos de retorno: e .
(E) Se a energia mecânica total for maior que zero, existirá apenas um ponto de retorno.
Passo 1
Temos um gráfico da energia potencial em função da distância entre duas partículas.
Tá difícil de imaginar como seria isso?
Uma dica... em uma situação como essa, não vale a pena queimar os neurônios imaginando uma possível situação real onde isso acontece.
Vamos analisar diretamente a energia potencial pelo gráfico, trabalhar diretamente com o resultado.
Mas para os curiosos... esse gráfico parece com a curva do potencial Lenard-Jones de uma ligação química.
Vamos olhar cada alternativa para achar a incorreta.
Passo 2
(A) O ponto de equilíbrio vale .
Pontos de equilíbrio são aqueles pontos de máximo ou mínimo local, por exemplo:
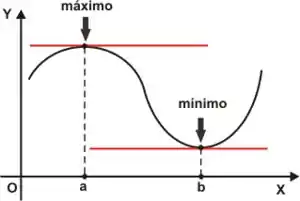
Então, no nosso gráfico podemos ver que o ponto é um ponto de mínimo local, logo é um ponto de equilíbrio.
A afirmativa (A) está correta.
Passo 3
(B) O ponto de equilíbrio é estável.
Para saber se o equilíbrio é estável ou instável, basta olhar se o ponto é de mínimo ou máximo local.
Como é um ponto de mínimo local, o ponto será um equilíbrio estável.
Isso acontece pois a força sempre tenta fazer o(s) corpo(s) voltar(em) ao equilíbrio.
A afirmativa (B) está correta.
Passo 4
(C) Se a energia mecânica total for igual a , a distância das partículas oscila em torno de .
Como o equilíbrio em é estável, a distância das partículas oscilaria em torno desse ponto.
PORÉMMM...
A energia total (mecânica) do sistema é exatamente a energia potencial do sistema nesse ponto .
Para qualquer um dos dois lados do gráfico, a energia potencial é maior do que em , isso sempre vai acontecer em um equilíbrio estável.
Assim, não há energia suficiente para o sistema sair desse equilíbrio, portanto, a distância não oscila.
A afirmativa (C) está incorreta.
Achamos a nossa resposta, mas vamos terminar de ver as alternativas.
Passo 5
(D) Se a energia mecânica total for igual a , existem dois pontos de retorno: e .
Como a energia total tem o valor de , a distância entre as partículas não vai conseguir passar daqueles dois pontos com esse valor e .
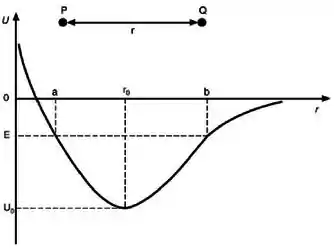
A afirmativa (D) está correta.
Passo 6
(E) Se a energia mecânica total for maior que zero, existirá apenas um ponto de retorno.
Se a energia mecânica for igual a zero, do lado esquerdo teremos um ponto de retorno (raiz do gráfico), em que a distância não conseguirá passar desse valor.
Entretanto, do lado direito, o gráfico parece nunca atingir o valor de zero, portanto não há um ponto de retorno desse lado.
Então, realmente, só há um ponto de retorno para o valor nulo de energia mecância.
A afirmativa (E) está correta.
Resposta
Letra (C)