A energia potencial de uma partícula que se move ao longo do eixo é dada por , onde está em joules e em metros. Se a energia mecânica total é os limites de seu movimento são:
(A) ; ;
(B) ; ;
(C) ; ;
(D) ; ;
(E) ; ;
Passo 1
Vamos lá, a energia mecânica total é .
Ahhh, mas que história é essa de energia negativa??
Calma, isso é só uma questão de referencial.
Por exemplo... Se eu coloco um referencial de energia potencial gravitacional zero em uma altura , um corpo abaixo dessa altura terá uma energia potencial gravitacional menor que zero, ou seja, “energia negativa”.
Okay, beleza!
Bom, a gente sabe que a energia mecânica total é a soma da energia cinética com a potencial:
Além disso, sabemos como a energia potencial varia ao longo do trajeto:
Então, sabemos qual parte dessa energia mecânica total estará na forma de energia potencial em cada ponto do trajeto.
Mas o que acontece quando a energia potencial atingir o valor de ?
Isso significa que toda a energia está na forma de energia potencial , ou seja, a energia cinética é zero. Assim, o corpo para, pois não tem velocidade para continuar o trajeto.
Isso é chamado um ponto de retorno, onde a energia potencial atinge o valor total de energia disponível (mecânica).
Então, os limites do movimento que queremos serão os pontos de retorno.
Passo 2
Para calcular esses pontos de retorno, basta igualar a função da energia potencial com o valor de energia total .
Então, é só acharmos as raízes desse cara que achamos os pontos onde a energia potencial tem o valor máximo, ou seja, os limites do movimento.
Passo 3
Para achar as raízes, vamos usar aquele cara lá... o Bhaskara.
Calculando o :
Aplicando a fórmula de Bhaskara:
Então, as raízes são:
Então, e são os dois limites de movimento da nossa partícula.
OBS: A função é uma parábola com concavidade para cima, pois o “a” é positivo. Por isso, o valor de nunca ultrapassa entre esses dois pontos.
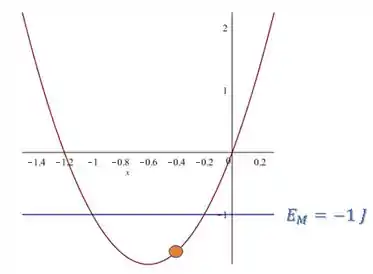
Ficamos com a alternativa (A).
Resposta
Letra (A)