Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa correspondente a um potencial , dado pela figura abaixo. Para este potencial, entre as opções abaixo, a única incorreta é:
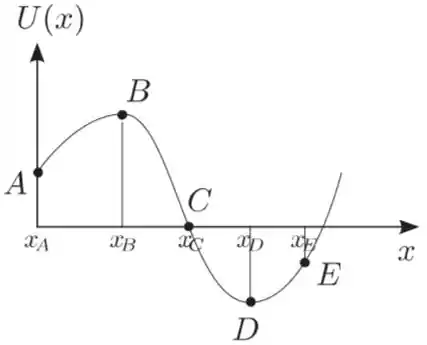
a) na posição a força sobre a partícula é nula;
b) na posição , tem-se a condição de equilíbrio estável;
c) no deslocamento do corpo de para a variação de energia cinética do corpo é positiva;
d) o sentido da força na posição é negativo;
e) na posição a força é nula.
Passo 1
Vamos analisar as opções uma a uma:
Alternativa : na posição a força sobre a partícula é nula.
Correta! Temos que lembrar que:
Lembrando-se da interpretação geométrica da derivada que quer dizer o ângulo da reta tangente à curva naquele ponto. Temos no ponto um instante em que o ângulo da reta tangente à curva é zero, ou seja, a derivada vai ser igual a zero e, portanto, a força também será nula.
Alternativa : na posição , tem-se a condição de equilíbrio estável.
Correto! Lembrando que o equilíbrio estável acontece nos “vales” das funções. Em outras palavras, equilíbrio estável é o ponto em que não importa para qual lado você mova a partícula, a força sobre a partícula sempre vai apontar para esse ponto de equilíbrio tentando restaurar ela para esse ponto. Utilizando a relação entre a força e a derivada da função que mostramos na alternativa anterior, vemos que ao se mover para direita, a derivada é positiva logo a força será negativa apontando para o ponto de equilíbrio. E movendo-se para a esquerda a derivada será negativa logo a força será positiva apontando para o ponto de equilíbrio.
Alternativa : no deslocamento do corpo de para a variação de energia cinética do corpo é positiva.
Correto! Vamos utilizar a conservação de energia mecânica.
Onde e .
Observando o gráfico vemos que , Logo .
Alternativa : o sentido da força na posição é negativo.
Correto! A derivada da função em é positiva, logo pela fórmula, a força sobre a partícula será negativa.
Alternativa : na posição a força é nula.
Falsa! Na posição a reta tangente tem uma inclinação negativa, ou seja, uma força positiva atuando sobre ela. Para ser uma força nula teria que ser um “vale” ou um “pico” da função, onde a reta tangente não faz angulação com o eixo .
Resposta
Alternativa