Conservação de Energia Mecânica
Um próton de massa se move em uma dimensão na presença de uma força cuja energia potencial é dada por:
Sendo e constantes positivas. O próton é liberado do repouso no ponto
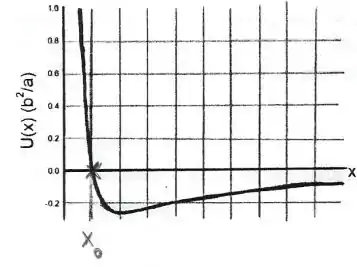
a) Calcule .
b) Escreva qual(is) é(são) o(s) ponto(s) de equilíbrio, e classifique-o(s) como estável, instável ou indiferente, fundamentando a classificação.
c) Calcule a velocidade do próton em função da posição .
Passo 1
a)
Se nós mexermos um pouco na fórmula da energia potencial, podemos facilitar esse conta:
Agora se substituirmos :
Passo 2
b)
Do gráfico, pode-se ver que há um ponto de equilíbrio estável em (um ponto de mínimo). Se não fosse possível ver o valor de naquele ponto, poderíamos também utilizar , igualando a força à zero.
Além disso, tem também um , ou seja, não é nem equilíbrio instável nem estável, é uma reta horizontal. Pelo gráfico, podemos ver que isso ocorre quando .
Passo 3
c)
A energia mecânica do próton é calculada por:
Em o próton é liberado do repouso, portanto, e como calculamos no item (a), , Logo .
Para , por conservação de energia mecânica, . Logo
Se utilizarmos a simplificação que fizemos no item (a):
Entretanto temos que :
Substituindo na equação:
Resposta
a)
b)
ponto de equilíbrio estável em
ponto de equilíbrio indiferente em
c)