Conservação de energia mecânica
Um corpo de massa se move em uma dimensão ao longo do eixo . Sua energia potencial é dada por:
Onde é dado em metros e em joules. O gráfico representa a variação da energia potencial em função da distância. Caso seja necessário, use .
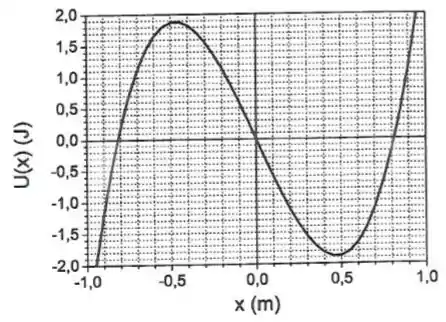
a) Calcule a força exercida sobre o corpo em função de .
b) Calcule a(s) posição(ões) de equilíbrio, marque-a(s) como ponto(s) de equilíbrio estável, instável ou indiferente. Justifique sua resposta.
c) Assumindo que o corpo esteja inicialmente no ponto de equilíbrio à direita da origem, a partir de qual valor para a velocidade o movimento deixa de ser oscilatório?
Passo 1
a)
Basta lembrar que a força é igual a menos a derivada da energia potencial.
Passo 2
Os pontos de equilíbrio ocorrem quando , então:
Esses dois pontos são representados nessa figura:
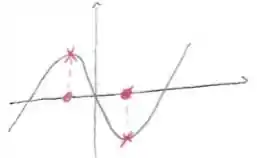
Passo 3
c)
O movimento deixa de ser oscilatório se o corpo alcançar o ponto de equilíbrio a esquerda da origem. Então vamos calcular a variação de energia cinética entre esses pontos para descobrir a velocidade necessária para alcançar o ponto de equilíbrio instável.
Resposta
a)
b)
c)