Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equilíbrios

Ver Teoria
Exercício 221234567891011121314151617181920212324252627282930313233

Enunciado

UFF, Física 1, Prova 1, 2016.1

Uma partícula se move na direção x sob a ação de uma força F ( x ) cuja energia potencial associada a ela é dada por U ( x )   = a x 2 - b x 3 . Quais são os pontos de equilíbrio associados a esta energia potencial?

(A) x   =   0   e   x   =   a / b  

(B) x   =   0   e   x   =   ( 2 a ) / ( 3 b )  

(C) x   =   a / b   e   x   =   ( 2 a / ( 3 b )

(D) x   =   0   e   x   =   -   ( 2 a ) / ( 3 b )  

(E) x   =   -   a / b   e   x   =   a / b

Passo 1

Então, galerinha! Essa é uma questão de energia potencial por deslocamento.

Sabemos que o gráfico de energia potencial por deslocamento tem essa cara:

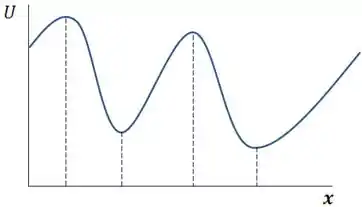
E a relação entre a força aplicada e a energia potencial é essa:

F = - d U d x

Bom, os pontos de equilíbrio acontecem justamente quando essa força é zero, ou seja, a derivada do gráfico é zero. Repare nas figuras que são os pontos de máximo e de mínimo.

No caso do problema, a função foi dada. Para descobrirmos os pontos de equilíbrio, vamos deriva-la e igualar a derivada da função a zero.

U x = a x 2 - b x 3

d U x d t = 2 a x - 3 b x 2

Igualando a zero:

2 a x - 3 b x 2 = 0

2 a x = 3 b x 2

x ' = 0

x ' ' = 2 a / 3 b

Resposta

(B) x   =   0   e   x   =   ( 2 a ) / ( 3 b )  

Exercícios de Livros Relacionados

A energia potencial entre dois átomos em uma molécula diatômica é dada por U r =a r 12 -b r 6 , onde r é a distância entre os átomos e a e b são constantes positivas. a) Determine a força F ( r ) que
Um peixe está preso em uma mola vertical, e quando ele é lentamente abaixado até atingir sua posição de equilíbrio a mola fica comprimida uma distância d. Quando o mesmo peixe está preso a essa mola e
Sua firma está projetando uma nova montanha-russa. Para a concessão do alvará de funcionamento, é exigido o cálculo de forças e de acelerações em vários pontos importantes do percurso. Cada carrinho t
Um bloco de madeira (massa m ) está ligado a duas molas sem massa, como mostrado na Figura 7-59. Cada mola tem um comprimento frouxo L e uma constante de força k . (a) Se o bloco é deslocado de uma di
Uma bola de gude move-se ao longo do eixo Ox. A energia potencial �� indicada na Figura 7.28. a) Para quais valores de x indicados no gráfico a força é igual a zero? b) Para quais valores de x indicad