Uma partícula de massa pode se deslocar em uma dimensão, submetida a um potencial dado por em unidades do SI: em Joules (), e em metros ().
Determine a expressão da força atuando sobre a partícula em função da posição .
Calcule as posições de equilíbrio da partícula.
Determine as condições de equilíbrio em cada ponto, ou seja, se é estável, instável ou indiferente.
Se uma partícula de massa for deixada na condição de equilíbrio estável com velocidade de , ela realiza um movimento periódico? Justifique.
Passo 1
Utilizando a relação:
Passo 2
As posições de equilíbrio ocorrem onde a derivada é zero, logo:
Resolvendo a equação do segundo grau temos duas soluções:
Passo 3
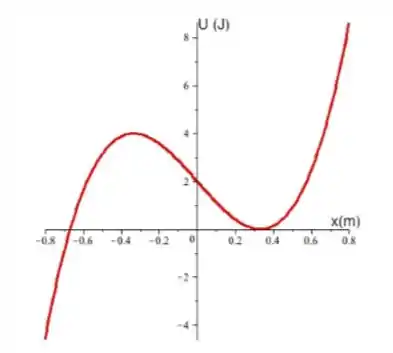
Basta observar o gráfico e ver o que acontece antes e depois do ponto de equilíbrio.
No ponto temos um ponto de máximo, ou seja, a função decresce antes e depois do ponto. Logo, é um ponto de equilíbrio instável.
No ponto temos um ponto de mínimo, ou seja, a função cresce antes e depois do ponto. Logo, é um ponto de equilíbrio estável.
Passo 4
O ponto é o ponto de equilíbrio, neste ponto, a energia potencial é zero segundo o gráfico. Logo a energia mecânica se dará apenas pela energia cinética:
Agora vamos analisar o gráfico, ao lado direito do ponto o gráfico cresce infinitamente, logo a partícula irá alcançar determinada energia e voltar ao ponto de equilíbrio. Entretanto, no lado esquerdo ao ponto o gráfico possui um ponto de máximo em que ele volta a decrescer depois. Esse ponto, segundo o gráfico possui energia potencial de , que é menor que , logo a partícula será capaz de passar por esse ponto e depois decrescer infinitamente, não retornando mais ao ponto .
Portanto, o movimento não será periódico.
Resposta
O ponto é um ponto de equilíbrio instável.
O ponto é um ponto de equilíbrio estável.
O movimento não será periódico.