Trabalho e Energia Cinética, Energia Potencial e Conservação de Energia
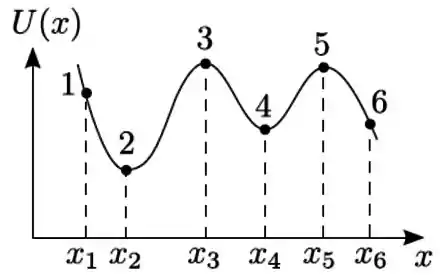
A figura mostra a energia potencial de uma partícula que move-se ao longo do eixo sob a ação da força resultante associada a . A alternativa FALSA é
(a) Na posição , tem-se a condição de equilíbrio estável;
(b) No deslocamento da partícula da posição para a posição , o trabalho realizado sobre a partícula é positivo;
(c) O sentido da força na posição é positivo;
(d) Na posição , a força sobre a partícula é nula;
(e) No deslocamento da partícula da posição para a posição , a variação da energia cinética é positiva.
Passo 1
Vamos ver as alternativas uma por uma!
Alternativa (a):
No gráfico de energia potencial pela posição, o equilíbrio estável acontece nos pontos de mínimo local, que nem o ou, justamente, o .
Ou seja, a alternativa é verdadeira. Mas a gente quer a falsa!
Passo 2
Alternativa (b):
Quando nos deparamos com uma alternativa dessas, perguntando o sinal do trabalho, temos que lembrar de uma coisa: que energia potencial perdida é trabalho ganho e vice versa. Afinal, a energia potencial é uma energia armazenada pela partícula que pode se transformar em trabalho.
Ou seja, se a energia potencial aumenta, o trabalho é negativo. E se a energia potencial diminui, o trabalho é positivo.
No gráfico, podemos ver que : a energia potencial aumentou. Então o trabalho realizado sobre a partícula é negativo.
Logo, a alternativa está errada.
Passo 3
Alternativa (c):
Quando o gráfico é decrescente, a força é positiva. E em o gráfico é decrescente, então o sentido da força é positivo, e a alternativa é verdadeira.
Passo 4
Alternativa (d):
Em qualquer ponto de equilíbrio (pontos de máximo e mínimo locais da função), a força é zero. O ponto é um ponto de máximo local, então nele a força sobre a partícula é nula.
Passo 5
Alternativa (e):
Vamos usar a mesma lógica que pra alternativa (b).
Da posição pra , a energia potencial diminui, então o trabalho realizado sobre a partícula é positivo. Portanto, a alternativa está correta.
Resposta
Alternativa (b)