Seja o plano , tal que sua equação paramétrica é:

Decida se é Verdadeiro ou Falso e justifique:

• A reta gerada pelo vetor intersecta
• Se , então para todo

Agora basta igualar as equações paramétricas:

Pela e , podemos ver que , assim vamos substituir na !

Logo, . Assim, podemos ver que a reta gerada pelo vetor intersecta o plano , quando e . Então, o primeiro item é VERDADEIRO.

A segunda é muito fácil! Sem fazer contas você já consegue visualizar que o plano é deslocado pelo vetor , assim ele não está na origem. Então este item é FALSO. Qualquer dúvida, tente igualar o vetor nulo a equação paramétrica do plano e achar se existem ... você verá que não existe!

Para a terceira afirmação, vamos seguir a mesma ideia do primeiro item, ou o que você faria no item anterior se tivesse com dúvida.

Agora basta substituir na primeira equação e verificamos que:

Então, de fato, o vetor pertence ao plano. Logo, o terceiro item é VERDADEIRO.

Este último item é um pouco mais difícil, tenho que admitir. De imediato você pensaria que a resposta é verdadeiro, né? Porque a noção de pertencer ao plano que todos nós temos é esta aqui:

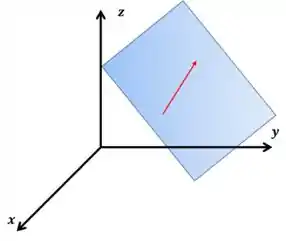
Entretanto, não é sempre isso que acontece. Lembra do vetor deslocamento?

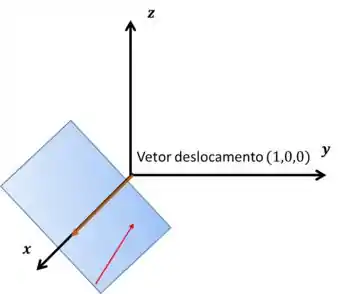
Perceba que se o vetor deslocamento “esticar” um pouco, ele vai “furar” o plano, por causa de um simples detalhe: o vetor não é a flecha inteira, apenas a pontinha da flecha! Mudou sua vida não, rs? Quando descobri isso, a minha mudou.

Não ta acreditando? Tente esticar o vetor deslocamento. Por exemplo, multiplique por e resolva o sistema!

O mesmo podemos aplicar para o vetor : tente multiplicá-lo por e ver se pertence ao plano (você verá que não). Logo, o item é FALSO.