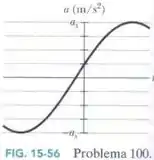
Qual é a constante da fase do oscilador harmônico cuja função aceleração aparece na Fig. 15-56 se a função posição é da forma e ?
Passo 1
Aqui a gente vai seguir o nosso esquema pra determinar a fase do oscilador. Porém, temos uma diferença: o nosso gráfico é da aceleração, já a função dada, do deslocamento.
Assim, precisamos lembrar que se:
Perceba que a gente apenas derivou ali em cima.
Passo 2
Agora vamos olhar no gráfico: o é a quarta divisão na escala vertical. Logo, como , cada divisão valerá
Pelo gráfico, a gente consegue perceber que o valor da aceleração quando vale .
Passo 3
Assim, podemos dizer que:
Repare que aqui o é a amplitude da aceleração, que vale:
Como o gráfico que temos é da aceleração, podemos usar o direto como a amplitude dele, porque já temos essa amplitude, sem precisar fazer . Beleza? Então:
Assim, considerando o intervalo de :
Também poderíamos ter: . E agora, como saber qual é o valor correto?
Passo 4
Bom, podemos pensar que a derivada da curva é dada por:
Em , essa derivada é igual a inclinação da reta tangente na curva nesse ponto. Podemos observar que essa inclinação é positiva, logo:
Como , temos que ter:
Logo, só o ângulo de satisfaz essa inequação.