UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 33b
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
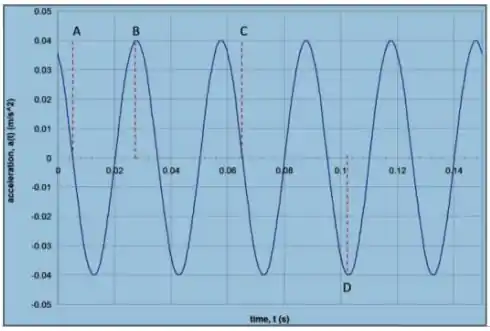
A velocidade máxima do corpo.
Passo 1
Oiie, tudo certinho contigo?
Temos o seguinte gráfico
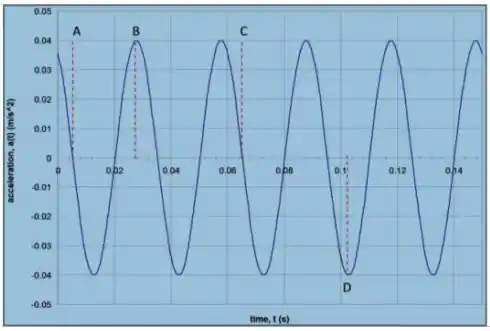
ele indica a aceleração em função do tempo de uma partícula de massa que está preso em uma mola! Ou seja, na ausência de atrito temos um movimento harmônico simples! Esta alternativa pede
A velocidade máxima do corpo.
Ou seja, a amplitude do movimento oscilatório! Esse gráfico é da aceleração, então temos que obter uma solução da forma
ou
qual iremos escolher é uma questão das condições iniciais do nosso problema! Temos que é o deslocamento máximo (a amplitude) da oscilação, é a frequência natural de oscilação e é a fase do movimento! Eventualmente todos terão que ser encontrados! Vamos analisar isso com calma! Na questão anterior obtemos que
a partir do que obtivemos
Vamos usar essas informações e o nosso gráfico para obter a nossa velocidade máxima!
Passo 2
A fase para esta alternativa não importa muito, portanto, vamos escolher qualquer uma de nossas soluções possíveis, temos que
se derivarmos esta expressão obtemos
O valor máximo é obtido quando
Se escolher a outra solução, o método é o mesmo, vamos você teria que igualar o cosseno à um. Temos que
Vamos usar agora os resultados da alternativa anterior! Saca só!
Passo 3
Usando que
e que
obtemos
Mais uma alternativa já era! Vamos para a próxima!