Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).
- Encontre a amplitude do movimento da sombra projetada no solo.
- Encontre o período e a frequência angular deste movimento.
- Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
- Faça um gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.
Passo 1
a)
Galera, aqui a gente precisa perceber apenas uma coisa: um MHS pode ser encarado como uma projeção de um MCU.
A figura abaixo ilustra isso:
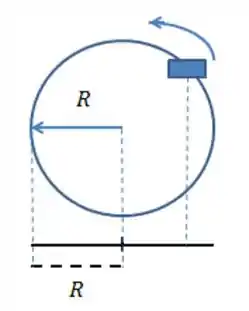
Tá vendo a linha preta embaixo do círculo? Essa é a representação do MHS.
Bom, com isso, podemos responder a primeira pergunta: qual a amplitude?
Pela figura, percebemos que a amplitude é o raio do círculo.
Então:
Passo 2
b)
Seguindo a mesma idéia de antes, é fácil perceber que o período, frequência e a frequência angular do movimento serão os mesmo que o do MCU.
Então, o período do MHS já está dado no enunciado.
Segundo o enunciado, a roda gigante completa uma volta a cada . Isso quer dizer que o período é justamente esse:
E a frequência angular é:
Passo 3
c)
A posição segue o modelo dos MHS e é dada por:
Já sabemos quase tudo, menos a fase ().
Bom, a informação que temos é que o movimento do carrinho, e de sua sombra, começa quando o carrinho se encontra no ponto mais alto da trajetória. Nesse caso, a projeção da sua sombra se encontra na origem do sistema que descreve o MHS( aquela linha preta lá de cima).
Então, depois de tanto blá blá blá, o que quero dizer é que:
Ou seja:
Show! Então:
Pra achar a velocidade e a aceleração, basta a gente derivar esse equação uma vez e depois derivar de novo:
Passo 4
d)
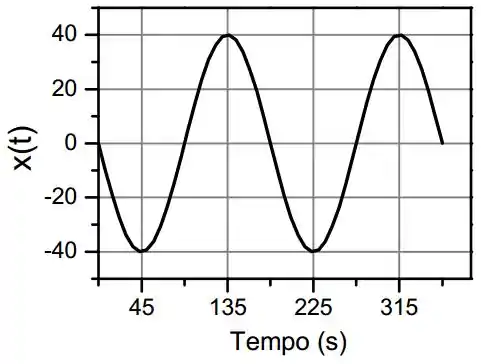
Basta a gente pegar sucessivos valores de tempo pra formar o gráfico:
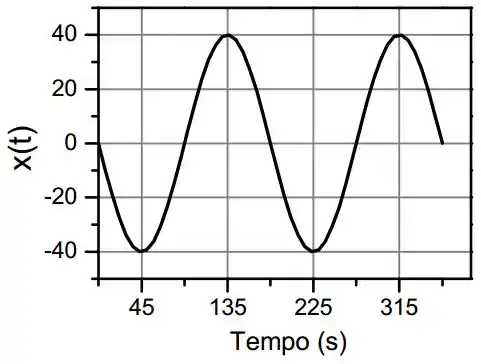
Resposta
a)
b)
c)
d)