Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 41.
(Cap 5 – Ex 41) APLICAÇÃO EM ENGENHARIA. Você participa de um rali em um dia nevoso, quando a temperatura está próxima do ponto de congelamento. O coeficiente de atrito estático entre os pneus do carro e a estrada congelada é 0,080, O chefe de sua equipe está preocupado com alguns dos morros do percurso e pede para você considerar a troca para pneus de neve. Para resolver a questão ele quer comparar os ângulos dos morros do percurso para ver quais deles seu carro consegue transpor
(a) Qual é o ângulo de inclinação máxima que um veículo com tração nas quatro rodas pode subir com rapidez constante?
(b) Se os morros estão congelados, qual é o ângulo de inclinação máxima para que o mesmo veículo com tração nas quatro rodas possa descer com rapidez constante?
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Para resolvermos o item (a), precisaremos apenas usar a definição de coeficiente de atrito estático e a 2ª Lei de Newton.
Mas calma aí, o que é o coeficiente de atrito estático mesmo?
No momento em que o objeto está parado, ênfase para parado, o número que representa a maior ou menor dificuldade imposta pela superfície ao movimento é denominado de coeficiente de atrito estático.
E a segunda lei de Newton, trata do que mesmo?
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração, ou seja, o famoso .
E para nos ajudar no exercício, como já é clássico para o Newton, usaremos um Diagrama de Corpo Livre para visualizarmos o sistema.
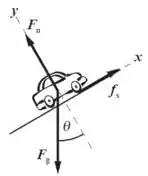
Adotaremos os eixos e representados no diagrama. Sendo a força normal do carro com o morro, a força de atrito entre o carro e o morro, que é o que empurra o carro para frente e o peso do carro, considere o ângulo a inclinação máxima do morro. Somando as forças em e em teremos que será igual a zero, isto é, a aceleração será nula que é o caso limite que estamos procurando (lembrando de decompor a força peso nesses eixos), temos:
Como , então das equações acima, podemos obter:
Passo 2
Usando a definição de coeficiente de atrito estático, que discutimos no começo do exercício, temos:
Até agora só brincamos com as variáveis para simplicar a equação. Agora substituiremos o valor de coeficiente de atrito estático fornecido pelo enunciado:
Passo 3
No item (b) temos uma certa pegadinha no conceito. Como não há informação de alteração do atrito estático para a descida, então temos exatamente o mesmo processo do item (a), porém em uma descida. Ou seja, desenvolvento o processo, obteremos o mesmo resultado:
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)