Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 83.
(Cap 5 – Ex 83) Você está girando sua irmã mais nova em um círculo de raio , como mostrado na figura. Se a massa dela é e você faz com que ela complete uma revolução a cada , (a) qual é a magnitude e a direção da força que deve ser exercida por você sobre ela? (b) Qual é a magnitude e a direção da força que ela exerce sobre você?
Passo 1
Falaaaaaaaaa galerinha do Responde ai, tudo joinha?
Bora resolver essa juntinho comigo?
Simboráaa
a) Olá! Então temos uma situação onde há movimento circular que pode ser esquematizada assim:
A gente imagina que sua irmã é uma partícula como diz no enunciado. E que como na foto a menina fica um pouco inclinada em relação ao solo, vamos imaginar que há essa inclinação entre o plano horizontal e a força que você exerce sobre ela para haver o movimento.
Como a gente quer descobrir essa força e sua orientação, vamos fazer um diagrama de corpo livre da situação:
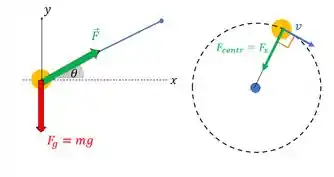
As componentes de são:
Percebe que para que haja uma trajetória circular, é necessário que acha uma força no plano da circunferência apontando para o centro da trajetória. Quem vai fazer esse papel é , porque o movimento da menina só ocorre no plano horizontal.
Ou seja, a ideia é ela gire apenas em um plano horizontal, ou seja, sem nenhum movimento no eixo , por isso queremos que haja equilíbrio na vertical. Pela segunda lei de Newton:
Passo 2
E na direção horizontal temos as forças que mantém a trajetória circular. Aplicando a segunda lei de Newton para direção :
Mas lembra que esse é a aceleração horizontal da força resultante sobre a pedra. Só que na horizontal temos um movimento circular e força resultante é uma força centrípeta, então a aceleração horizontal é a aceleração centrípeta, que é dada por . Substituindo:
E para o movimento circular, temos essa fórmulinha para a velocidade :
Já que a trajetória é uma circunferência de raio , e o tempo de percurso é o tempo de revolução . Substituindo isso na equação anterior:
Passo 3
Temos um sistema de equações formado por e :
Percebe que ele relaciona só quem a gente quer, com a orientação dela . Então precisamos apenas resolver esse cara.
Dividindo a primeira equação pela segunda ficamos com o seguinte resultado:
Substituindo os dados e isolando :
Passo 4
E agora podemos substituir isso em qualquer uma das equações para encontrar o módulo de :
E a direção dessa força está indicada no desenho, forma um ângulo de com a horizontal no sentido anti-horário.
Passo 5
(b) A terceira lei de Newton diz que se um corpo 1 exerce uma força sobre o corpo 2, o corpo 2 vai exercer sobre o corpo 1 uma força de magnitude igual e sentido oposto.
Assim a força que a criança exerce sobre você tem a mesma magnitude e direção, mas sentido oposto.
Ou seja, ela exerce , mas dessa vez formando um ângulo de com a horizontal.
Resposta
(a) A força é de , formando .