Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 51.
(Cap 5 – Ex 51) Dois blocos ligados por um cordão (figura abaixo) deslizam para baixo sobre um plano inclinado de . O bloco 1 tem a massa e o bloco 2 tem a massa . Ademais, os coeficientes de atrito cinético entre os blocos e o plano são , para o bloco 1 e para o bloco 2. Encontre
(a) a magnitude da aceleração dos blocos e
(b) a tensão no cordão.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Começando o item (a).
Como precisamos encontrar a magnitude da aceleração dos blocos, podemos utilizar a segunda lei de Newton.
Mas, a segunda lei de Newton diz o que mesmo?
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração, ou seja, o famoso .
E para nos ajudar no exercício, como já é clássico para o Newton, usaremos os Diagramas de Corpo Livre para visualizarmos os sistemas nos dois blocos.
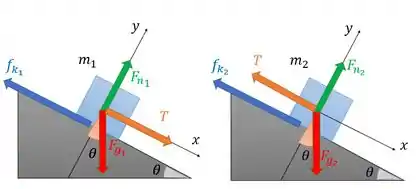
Temos a tensão onde temos a corda, temos a força peso para baixo nos dois casos e também temos a força normal , já que há contato entre os blocos e a superfície. Para finalizar temos a força de atrito cinético contrária ao movimento.
Como ambos os blocos estão somente sob a ação gravitacional como meio de força externa, então eles devem estar descendo a rampa. Assim a força de atrito aponta para o subir da rampa, no sentido contrário ao movimento.
Os dois blocos vão descer com a mesma aceleração já que estão ligados por um fio tensionado (esticado).
Nossa missão, então, é encontrar .
Passo 2
A segunda lei de Newton para o bloco no eixo fica:
Sendo que é a magnitude da aceleração dos blocos. Nessa direção temos a tensão no sentido de , temos a componente de que será , entrando no somatório como uma força positiva. Como :
E temos também a força de atrito cinético nessa direção. Ela tem a expressão , apontando para , e ficando como uma força negativa no somatório. Portanto:
Já para o eixo teremos que , por não haver movimento nessa direção. Nela temos e , que entrará negativa no somatório por apontar para . Portanto:
Aplicando a equação (2) em (1):
Passo 3
Faremos o mesmo raciocínio nesse passo, porém para o bloco 2.
As equações de e ficam quase iguais. A diferença é que a massa agora é (vamos mudar isso e os demais índices de 1 para 2) e a tensão está no sentido inverso de , ficando negativa na equação da segunda lei de Newton desse eixo.
Para o eixo , teremos portanto:
E para o eixo , a equação ficará igual ao do outro bloco, apenas mudaremos os índices:
Aplicando a equação (5) em (4):
Passo 4
Ainda não queremos encontrar a tensão (isso fica para o item (b)), só a aceleração. E temos essas duas equações a partir de cada bloco:
Perceba como podemos excluir quando somamos a equação (3) com (6):
Vamos isolar :
Passo 5
Para esse passo, ficamos com a missão de inserirmos os valores do enunciado:
Perceba que esse resultado negativo representa o sentido da aceleração e não que equivale a algo menor que zero. Isso é muito importante. Essa aceleração negativa diz que os blocos estão perdendo velocidade enquanto deslizam.
A magnitude dessa aceleração nada mais é que o tamanho escalar dessa grandeza. Portanto tiramos o módulo desse valor:
Passo 6
Finalmente chegamos na letra (b).
Como conhecemos , podemos substituir em uma das equações que temos para definir o valor de . Vamos usar (3):
Substituindo os valores, lembrando de usar negativo:
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)