(Cap 5 – Ex 71) Seu time de engenheiros de teste está prestes a soltar o freio de estacionamento de um carro de , de forma que ele irá descer por uma inclinação muito longa de em preparação para uma batida no fim da rampa. (Em uma inclinação de , a mudança na altitude é da distância horizontal viajada.) A força resistiva total (arrasto do ar e atrito de rolamento) para esse carro foi estabelecida previamente como , onde é a rapidez do carro. Qual é a rapidez terminal para o carro descendo por essa inclinação?

Falai pessoal, tudo na paz?

Bora resolver essa comigo?

Simborá!!!

A força resultante sobre um objeto é zero se o corpo estiver em repouso ou em movimento uniforme.

A segunda lei de Newton afimra que a força resultante exercida sobre o objeto é diretamente proporcional à sua massa e à aceleração. A expressão para a força resultante exercida sobre o objeto é

Vamos começar entendendo bem o que podemos tirar dessa inclinação de “”. Isso quer dizer apenas que a tangente do ângulo de inclinação da rampa é ,:

Beleza, então estamos em um plano inclinado e conhecemos o valor de , como fica o diagrama das forças que agem sobre o carro?

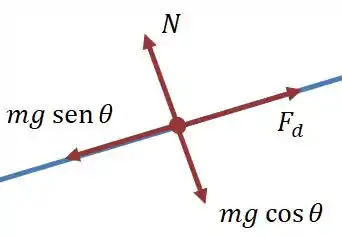
Um segundo diagrama para melhor visualização

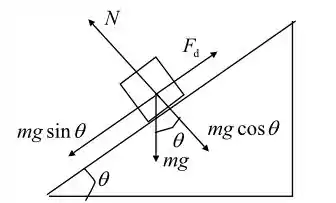
Vamos aplicar a segunda lei de Newton à direção paralela ao plano:

E substituindo com a expressão para que foi dada no enunciado:

Ok, essa é a equação dinâmica do carro.