Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 57.
(Cap 5 – Ex 57) Um bloco de desliza sobre o topo de um bloco de . O bloco de tem uma aceleração de enquanto uma força horizontal de é aplicada a ele, como mostra a figura abaixo. Não existe atrito entre o bloco de e a superfície horizontal, mas existe atrito entre os dois blocos.
(a) Encontre o coeficiente de atrito cinético entre os blocos.
(b) Encontre a aceleração do bloco de durante o tempo em que o bloco de permanece em contato com ele.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Começaremos avaliando o item (a).
Mais uma vez começaremos com o Diagrama de Corpo Livre dos sistemas. Já é um clássico do Newton, né?
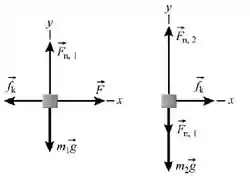
Lembrando que nesse momento definimos os nossos eixos e , fundamentais para conseguirmos aplicar a segunda lei de Newton.
Mas espera aí... Qual era a segunda lei mesmo?
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração, ou seja, o famoso .
Para deixar claro, o bloco 1 é o da esquerda e o bloco 2 é o dá direita, ok?
Vamos iniciar observando o que acontece nos eixos e no bloco 1:
Agora em :
Unindo as equações (1) e (2):
Podemos, agora, isolar o :
Por fim, substituindo os valores dados pelo enunciado:
Passo 2
Entraremos agora no item (b).
Basicamente aplicaremos a segunda lei de Newton em .
Ou seja:
Aplicando a equação (1) em (3), teremos:
Isolando :
Agora só falta substituir os valores:
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)