Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 63.
(Cap 5 – Ex 63) Um bloco de de massa repousa na superfície inclinada de uma cunha de de massa, como na figura. Uma força horizontal é aplicada sobre a cunha, que desliza sobre uma superfície sem atrito.
(a) Se o coeficiente de atrito estático entre a cunha e o bloco é e a cunha tem uma inclinação de com a horizontal, encontre os valores máximo e mínimo da força para os quais o bloco não escorrega.
(b) Repita a parte (a) com .
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Começando o item (a).
Como precisamos encontrar a Força que o bloco não escorrega, podemos utilizar a segunda lei de Newton.
Mas, a segunda lei de Newton diz o que mesmo?
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração, ou seja, o famoso .
E para nos ajudar no exercício, como já é clássico para o Newton, usaremos o Diagrama de Corpo Livre para visualizarmos o sistema nesse bloco.
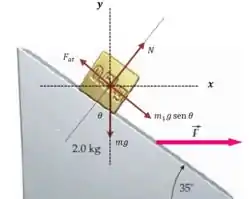
Vamos determinar as equações das Forças, começando pelo eixo :
E para o eixo :
Passo 2
O que colocamos na equação da força horizontal é a aceleração do sistema inteiro (bloco e cunha), ou seja:
E queremos achar os valores máximo e mínimo dessa força para que o bloco não deslize.
Quando a força é mínima, a preocupação é que o bloco não deslize para baixo, então temos que garantir que o atrito é forte o suficiente para segurá-lo onde está:
Substituindo na equação das forças verticais:
E agora aplicaremos isso tudo que descobrimos na equação das forças horizontais:
Dividindo todos os fatores por e isolando :
E esse será o valor mínimo da aceleração, e a força mínima associada é:
Passo 3
E para encontrar o valor máximo é só inverter a lógica. Agora nossa preocupação é que o bloco deslize para cima, então queremos garantir que a força de atrito estático (agora apontando para baixo) é suficiente para segurá-lo onde está:
Nem precisamos refazer a conta toda, é só inverter o sinal dos termos em que o aparece (que afinal de contas são os termos ligados à força de atrito):
E essa é a aceleração máxima, associada à seguinte força:
Passo 4
Para o item (b) só precisamos refazer as contas para o caso em que . Já temos as fórmulas prontas, apenas alteraremos os valores.
Para a força mínima temos:
E para a força máxima:
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a) e , com .
b) e , com .