Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 50.
(Cap 5 – Ex 50) Você e seu melhor amigo fazem uma aposta. Você alega poder colocar uma caixa de encostada a um dos lados de um carrinho, como na figura abaixo, sem que a caixa caia no chão, mesmo você garantindo que não fará uso de ganchos, cordas, prendedores, ímãs, cola ou qualquer outro tipo de adesivo. Quando seu amigo aceita a aposta, você começa a empurrar o carrinho no sentido mostrado na figura. O coeficiente de atrito estático entre a caixa e o carrinho é .
(a) Encontre a menor aceleração com a qual você vencerá a aposta.
(b) Qual é a magnitude da força de atrito, neste caso?
(c) Encontre a força de atrito sobre a caixa se a aceleração é duas vezes a mínima necessária para que a caixa não caia.
(d) Mostre que, para uma caixa de qualquer massa, a caixa não cairá se a magnitude da aceleração para a frente for , onde é o coeficiente de atrito estático.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Começaremos avaliando o item (a).
Mais uma vez começaremos com o Diagrama de Corpo Livre do sistema. Já é um clássico do Newton, né?
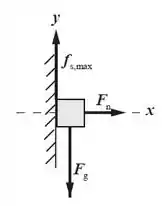
Lembrando que nesse momento definimos os nossos eixos e , fundamentais para conseguirmos aplicar a segunda lei de Newton.
Mas espera aí... Qual era a segunda lei mesmo?
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração, ou seja, o famoso .
O que deve acontecer é que a aceleração deve ser grande o suficiente para que a força de atrito consiga ser igual ao peso da caixa. Só que quando a aceleração é a mínima possível, a força de atrito estática é a máxima. Pensando assim, vamos usar a segunda lei de Newton para a caixa em e em , começando com .
Ou seja:
Portanto:
Porém , correto?
Porém a força de atrito é máxima, lembra? Então . Substituindo na nossa equação:
Passo 2
Agora precisamos pensar no que estará acontecendo no eixo :
Juntando as equações (2) e (3):
Podemos rapidamente cortar e isolar :
Substituindo os valores dados no enunciado:
Passo 3
Começando a letra (b), retornaremos com a equação (1):
Substituindo os valores do enunciado:
Passo 4
Partindo para o item (c), precisaremos ser bem conceituais.
Vamos avaliar os acontecimentos:
Já conhecemos qual é a aceleração mínima para que a caixa não caia. Se aumentarmos a aceleração, a caixa cairá? A resposta é não, já que aumentando a aceleração ela será obrigatoriamente maior que a aceleração MÍNIMA. E é possível que a caixa suba? Também não. Para que a caixa subisse, a força de atrito deveria ser maior que o peso da caixa. Porém o que acontece fisicamente é que a força de atrito se iguala ao peso da caixa, mas por nenhuma hipótese ultrapassa o peso. Portanto, a nossa única alternativa é que a força de atrito continuará igual ao peso da caixa:
Passo 5
Para finalizar, vamos observar a letra (d).
Mostramos no item (a) que a menor aceleração que impede a queda do bloco é e esse valor não depende da massa. Então, se a aceleração for ainda maior que esse valor, o bloco continua não caindo, qualquer que seja a massa.
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)
c)
d) A aceleração é maior do que a mínima necessária.