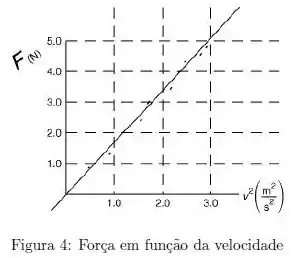
A força de resistência do ar sobre uma massa obedece à equação , onde é a velocidade da massa, para o intervalo de velocidades estudado em um experimento. Um gráfico de (em ) em função de (em ) é mostrado abaixo. Qual é o valor aproximado de ?
(a)
(b)
(c)
(d)
(e)
Passo 1
Dá uma olhada nessa função de :
Para quem não está acostumado, é esquisito pensar que o gráfico disso pode ser uma reta.
Isso porque, se pensarmos no gráfico de , teríamos uma parábola. Porém, quando colocamos a escala do eixo horizontal como , conseguimos linearizar essa curva, já que é proporcional ao quadrado da velocidade.
Assim, o gráfico de é uma reta e seu coeficiente angular (inclinação) é .
Passo 2
Para encontrar , vamos aproximar um ponto da reta, por exemplo esse aqui:
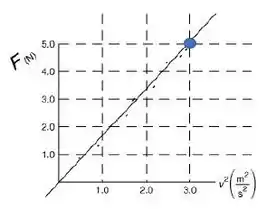
Agora basta calcular esse coeficiente angular com:
Passo 3
Mas qual a dimensão de ?
Vamos analisar as dimensões de cada parâmetro.
Então a análise dimensional fica assim:
Mas nenhuma resposta tem a unidade Newton envolvida. Então, vamos escrevê-la de uma outra maneira:
Substituinndo em nossa análise, temos:
Então conseguimos achar o valor de e sua dimensão:
Ficamos com a letra (b).
Resposta
Letra (b)