Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 45.
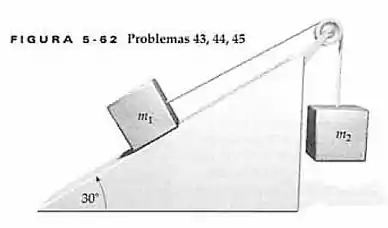
(Cap 5 – Ex 45) Na Figura abaixo, , e o coeficiente de atrito cinético entre o plano inclinado e o bloco de é . Encontre a magnitude da aceleração das massas e a tensão na corda.
Passo 1
Falaaaaaaaaa galerinha do Responde ai, tudo joinha?
Bora resolver essa juntinho comigo?
Simboráaa
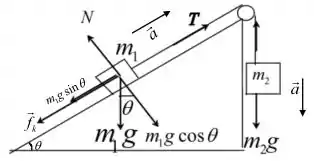
Escolhemos um sistema de coordenadas no qual a direção +x esteja no sentido de subida da rampa. Vamos supor que a sem massa e que está sempre esticada. Sobre a influência das forças mostradas nos diagramas de corpo livre abaixo, os blocos terão uma aceleração comum A aplicação da segunda lei de Newton a cada bloco, seguida da eliminação da tensão e o uso da definição de força de atrito cinética , nos permitirá determinar a aceleração do sistema.
Seguindo o D.C.L ,temos
Passo 2
Aplicando a 2° Lei de Newton no 1° bloco, temos:
E
Como
,
,
Então
Passo 3
Aplicando a 2° Lei de Newton no 2° bloco, temos:
Como então:
Somando essa última equação com a última do passo 2, temos:
Substituindo os valores numéricos que já temos:
Passo 4
Agora, basta resolver a equação que tínhamos anteriormente: