Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 62.
(Cap 5 – Ex 62) Um bloco de em um plano inclinado está preso a outro bloco de massa através de uma corda, como nas figuras. Os coeficientes de atrito estático e cinético para o bloco e o plano inclinado são e e o plano é inclinado a com a horizontal.
(a) Determine o intervalo de valores para , a massa do bloco pendurado, para os quais o bloco de não vai se mover a menos que seja perturbado, mas caso seja, vai deslizar para baixo pelo plano inclinado.
(b) Determine um intervalo de valores para para os quais o bloco de não vai se mover a menos que seja perturbado, mas caso seja, vai deslizar para cima pelo plano inclinado.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Começaremos avaliando o item (a).
A primeira coisa a ser feita é analisar o caso em que o bloco está parado, mas tendendo a deslizar para baixo.
Para isso vamos supor que o bloco estivesse deslizando pelo plano sem estar preso à massa :
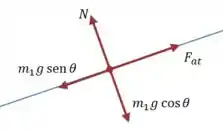
Consideraremos o eixo como o plano inclinado e, portanto podemos considerar, também, que a somatória de forças no eixo é:
Onde é o ângulo entre (Força gravitacional) e o nosso eixo .
Portanto:
Se essa força for maior do que zero, o bloco estará acelerando para baixo:
Podemos dividir os dois lados por e isolar o
Como o nosso coeficiente de atrito estático é , já garantimos que o bloco não vai entrar em movimento a menos que seja empurrado (do contrário vai permanecer em equilíbrio, porque o atrito vai ser suficiente para conter o peso).
Como o coeficiente de atrito cinético é , então o bloco vai acelerar para baixo caso seja empurrado.
Isso quer dizer que a massa mínima para satisfazer o item (a) é .
Passo 2
Ainda no item (a), vamos procurar a massa máxima que satisfaz a condição.
Nesse caso temos que colocar a tensão na corda (que é igual ao peso e puxa o bloco para cima no nosso sistema) na nossa conta:
E usando a mesma condição de antes:
A ideia é que a tensão na corda não supere o efeito do peso do bloco menos o atrito:
E o intervalo permitido para a massa , nesse caso é:
Passo 3
No item (b), vamos analisar o caso em que o bloco tende a subir o plano. Dessa vez a força de atrito vai apontar na mesma direção da força peso:
E pelo sistema de referência que escolhemos, a força resultante deve ser menor que zero para que o bloco tenha tendência a subir:
E estamos considerando que o bloco possa se mover plano acima, então usamos .
E para garantir que o bloco não se mova a menos que seja empurrado, a combinação da força peso com o atrito estático deve ser maior do que a tensão na corda:
E, então, o intervalo permitido para a massa nesse caso é:
Ah, como a Física é linda!
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)