Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 66.
(Cap 5 – Ex 66) (a) Um bloco está deslizando para baixo em um plano inclinado. O coeficiente de atrito cinético entre o bloco e o plano é . Mostre que o gráfico de em função de (onde é a aceleração ao longo da descida e é o ângulo de inclinação do plano em relação à horizontal) seria uma linha reta com inclinação e intercepto . (b) Os dados a seguir mostram a aceleração de um bloco deslizando por um plano inclinado como uma função do ângulo de inclinação do plano com a horizontal.
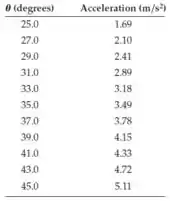
Usando um programa de planilhas, faça um gráfico desses dados e ajuste uma linha reta a eles para determinar e . Qual é a diferença percentual entre o valor obtido para e o valor usual de ?
Passo 1
Falaaaaaaaaa galerinha do Responde ai, tudo joinha?
Bora resolver essa juntinho comigo?
Simboráaa
Quando um bloco desce por um plano inclinado, o diagrama de forças é da seguinte forma:
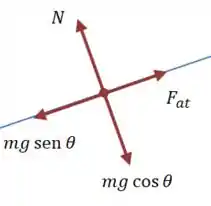
E aplicando a segunda lei de Newton na direção (paralela ao plano):
E agora, isolando a aceleração :
Passo 2
(a) Agora vamos escrever uma função que relacione (explicitamente) e .
Dividindo tudo por :
Que é exatamente a função de uma reta em que e :
Então é a inclinação e é o intercepto.
Passo 3
(b) Agora vamos usar um programa de planilhas para fazer um gráfico dos dados mostrados na tabela.
Para cada ponto no gráfico, a coordenada vertical vai ser dada por e :
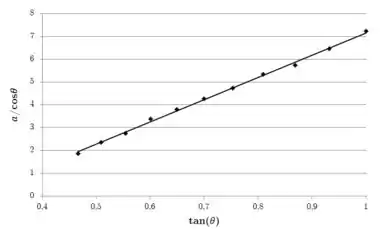
E podemos usar o próprio programa de planilhas para calcular a inclinação da reta que melhor se ajusta a esses pontos:
E então:
Passo 4
Agora vamos calcular a diferença percentual entre o valor calculado para e o valor usual:
Resposta
(a) Demonstração.
(b) e .
(c) .