P3 de Álgebra Linear da UFRJ - 2018.2

Encontre o modelo quadrático da forma que melhor se ajusta (no sentido dos mínimos quadrados) aos dados experimentais da tabela abaixo. Assinale o valor do coeficiente a.

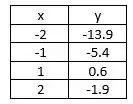
(a) 1

(b) 2

(c) -1

(d) -2

Seja a transformação , e seja um paralelepípedo. O volume do paralelepípedo transformado T(Q), em relação ao volume de Q:

(a) É o mesmo.

(b) É maior.

(c) É menor.

(d) Pode ser maior ou menor, dependendo de Q.

Calcule o determinante da matriz abaixo:

(a)

(b)

(c)

(d)

Calcule , onde é o ângulo formado por e

(a)

(b)

(c)

(d)

Seja e e

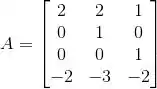
tal que . Então a projeção ortogonal de sobre a imagem de é:

(a)

(b)

(c)

(d)

Assinale o polinômio característico da matriz A.

(a)

(b)

(c)

(d)

Seja uma matriz cujas colunas são os vetores e Considere a matriz , cujas colunas são os vetores e Então:

(a)

(b)

(c)

(d)

Calcule a projeção ortogonal do vetor sobre o espaço gerado por e

(a)

(b)

(c)

(d)

Considere as afirmativas:

(I) Existem vetores e em tais que e

(II) Quaisquer que sejam os vetores e em ,

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja A uma matriz simétrica e a forma quadrática associada. Suponha que A não tenha autovalores nulos e que A possua pelo menos um autovalor positivo e um autovalor negativo. Então:

(a) Existem infinitos vetores x tais que

(b) Para todo x não nulo,

(c) Dependendo de A, pode existir ou não um vetor x não nulo tal que

(d) Para todo x não nulo,

Seja A uma matriz . Considere as afirmativas:

(I) Se , então

(II)

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Considere a seguinte base ortogonal de

Considere e seja o vetor de coordenadas de com relação à base Assinale abaixo o valor da primeira entrada de

(a)

(b)

(c)

(d)

Seja A uma matriz Assinale a única alternativa FALSA:

(a) é simétrica.

(b)

(c) é diagonalizável.

(d)

Seja A uma matriz e considere as afirmativas.

(I) Para todo existem e tais que

(II) Para todo existem únicos vetores e tais que e

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

A matriz possui dois autovalores distintos, e Sabe-se que é uma base do autoespaço associado a e é uma base do autoespaço associado a . Considere as afirmativas:

(I) Se e , então A é simétrica.

(II) Se e então A é simétrica.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.