Seja e e
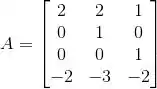
tal que . Então a projeção ortogonal de sobre a imagem de é:
(a)
(b)
(c)
(d)
Passo 1
Bom, lembra do método dos mínimos quadrados??
A gente tinha essa formulazinha:
Nela, A é uma matriz cujas colunas formam o espaço em que a gente quer projetar, é o vetor que a gente quer projetar e é um vetor cujas entradas dão a melhorar projeção e é também a nossa incógnita.
A gente viu que, quando a gente encontra o z e multiplica de volta pela matriz A, obtemos a projeção de no espaço gerado pelas colunas de A.
Mas lembra que o espaço gerado pelas colunas de A também é mais conhecido como imagem de A!
Então o que a gente quer achar na verdade é:
Mas como a gente faz isso com os dados do enunciado??
Passo 2
Vamos começar manipulando um pouco a fórmula de mínimos quadrados.
Multiplicando à esquerda dos dois lados por
Mas:
Então:
E foi isso que o enunciado deu pra gente né!
Então é só fazer:
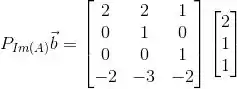
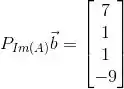
Resposta
(a)