Seja A uma matriz Assinale a única alternativa FALSA:
(a) é simétrica.
(b)
(c) é diagonalizável.
(d)
Passo 1
Para resolver essa questão, vamos pegar uma matriz qualquer.
Vou escolher a matriz:
Agora vamos testar cada alternativa para essa mesma matriz A.
(a) é simétrica.
Vamos calcular
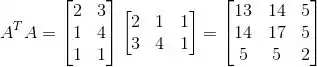
Essa matriz é simétrica!
Então a afirmativa (a) é verdadeira.
Mas não vamos marcar ela porque queremos a falsa!
Passo 2
(b)
Vimos que:
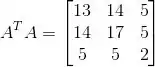
A imagem dessa matriz é o espaço gerado pelas colunas, que está no
Enquanto isso, a imagem da matriz A (espaço gerado pelas colunas de A) está no
Então não tem como dizer que os dois são iguais.
Por isso essa afirmativa é falsa e é a nossa resposta.
Passo 3
(c) é diagonalizável.
Vimos no passo 1 que é simétrica.
Logo, pelo Teorema Espectral, vai ser diagonalizável.
A afirmação é verdadeira.
Passo 4
(d)
O núcleo da matriz A é a solução do sistema homogêneo:
E o núcleo da matriz é a solução do sistema homogêneo:
Então, os vetores que zerarem a primeira equação também zeram a segunda, pois:
Logo, os núcleos dessas duas matrizes são iguais e a afirmação também é verdadeira.
Resposta
(b)