Assinale o polinômio característico da matriz A.

(a)
(b)
(c)
(d)
Passo 1
O polinômio característico é aquele cara que achamos quando fazemos:
Vamos começar achando quem é essa matriz e depois calculamos o determinante dela.
Temos:
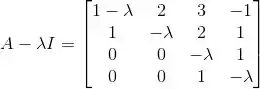
Beleza, agora precisamos achar o determinante dessa matriz!
Passo 2
Uma forma esperta de calcular o determinante de matrizes de dimensão maior que 3 é usando o escalonamento.
Quando temos uma matriz triangular, o determinante dela é o produto dos elementos da diagonal principal. E quando escalonamos uma matriz, obtemos uma matriz triangular superior!
Mas temos que tomar cuidado com algumas coisinhas:
- Quando você troca linhas ou colunas, o sinal do determinante muda;
- Quando você multiplica uma linha por um escalar, o determinante fica multiplicado por esse escalar;
- Se você troca uma linha/coluna pela soma dessa linha/coluna com um múltiplo de uma outra, o determinante não se altera.
Então vamos escalonar a matriz que achamos antes pra achar o determinante!
Passo 3
Escalonando:
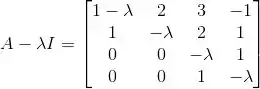
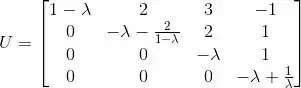
Agora temos uma matriz triangular superior, e para obtê-la só fizemos operações que não alteram o determinante da matriz inicial!
Logo:
Mas queremos que:
Logo:
Simplificando:
Resposta
(b)