P2 de Física 1 da USP - 2020.1

Uma partícula move-se ao longo do eixo x sob a ação de uma única força conservativa, que dá origem à energia potencial

onde é medido em metros e é medido em joules. O trabalho, em Joules, realizado pela

força quando a partícula se movimenta de até é:

Um sistema possui duas partículas que movimentam-se no plano . No instante, o centro de massa do sistema tem vetor posição , pois uma das partículas com massa está na origem e a outra, com massa , tem vetor posição . Sabendo que a velocidade instantânea do centro de massa do sistema é dada por , podemos afirmar que o módulo da força externa resultante que atua no sistema no instante , em Newtons, é:

A força resultante age sobre uma partícula de massa , que move-se ao longo do eixo , de tal forma que a sua posição em função do tempo é dada por:

com em metros e em segundos. O trabalho realizado pela força sobre a partícula de

s até s, em Joules, é?

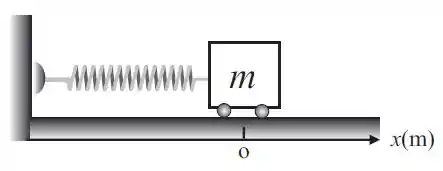
Uma mola tem uma extremidade fixa em uma parede vertical e a outra num carrinho de massa , que se movimenta como uma partícula numa superfície horizontal sem atrito sujeita a uma força elástica dada por . Se o carrinho passa pela posição com velocidade , sua velocidade escalar ao passar pela posição , em metros por segundo, é:

Um sistema é composto por duas partículas que se movimentam em um plano horizontal . Em um dado instante , observa-se que as duas partículas, de massas e , partem da origem do sistema de coordenadas, com velocidades e , respectivamente. Sabendo-se que elas estão sujeitas somente a forças internas, o módulo do vetor posição do centro de massa (em metros) quando é:

6. Um pequeno drone está navegando numa dada altura constante quando, por causa de um defeito de fabricação, explode em dois fragmentos. Imediatamente após a explosão, verifica-se que um dos fragmentos com massa , move-se com velocidade e o outro fragmento, de massa , move-se com velocidade , ambas velocidades medidas no mesmo referencial inercial em repouso. A velocidade escalar do drone antes da explosão, em metros por segundo, medida no mesmo referencial inercial é:

7. Uma partícula move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial

onde é medido em metros e é medido em Joules. Se a partícula parte da posição e movimenta-se na direção de crescente com energia mecânica total, a coordenada do ponto de retorno, medida em metros, é:

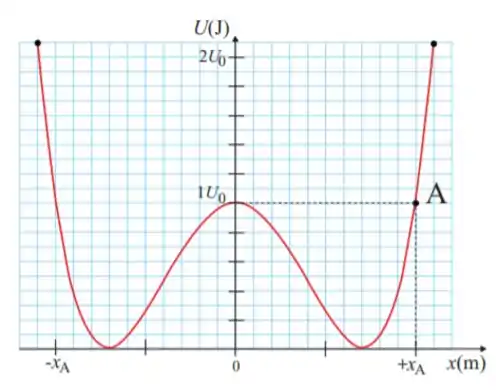
8. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial mostrada no gráfico abaixo. Se a partícula passa pelo ponto A de coordenada com velocidade escalar , a sua velocidade escalar quando passa por um ponto de equilíbrio estável, em metros por segundo, é aproximadamente:

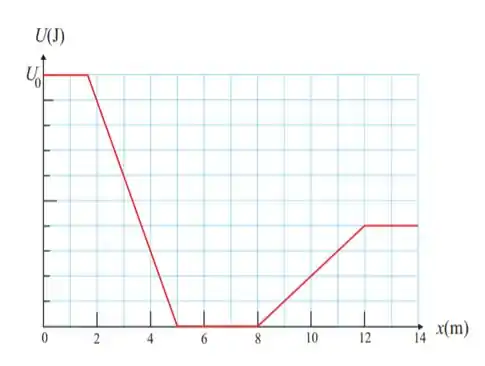
9. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial representada na figura abaixo onde a escala no eixo é definida por . Se a partícula é liberada em com energia , a sua velocidade escalar, em , na posição , é:

11. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível) conectada a um bloco de massa , que se move com velocidade . Durante o processo de colisão, quando a velocidade do bloco é , a energia potencial elástica armazenada na mola é:

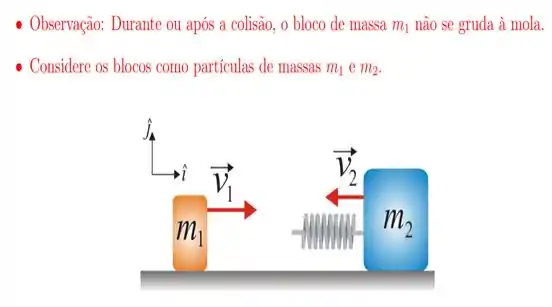
12. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível), de constante elástica , conectada a um bloco de massa , que se move com velocidade . Sabe-se que na máxima compressão da mola , os blocos têm a mesma velocidade. O valor da máxima compressão da mola, em centímetros, é dada por:

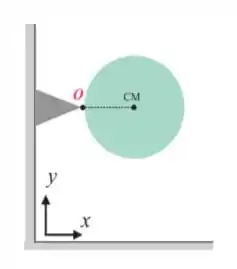
13. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor aceleração angular do disco no instante em que ele é abandonado, em , é:

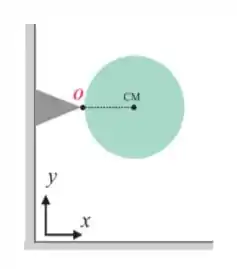
14. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor O módulo do vetor velocidade angular do disco quando seu centro estiver diretamente abaixo do eixo de rotação é, em :

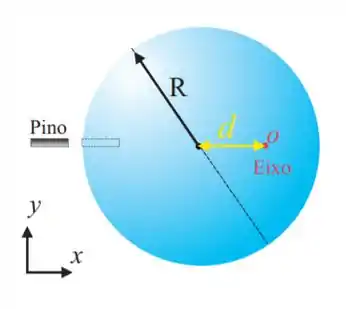
15. Um disco homogêneo de raio e massa está fixo por um pino a uma parede vertical no plano , conforme a figura abaixo. O disco pode girar, sem atrito, ao redor do eixo fixo que é perpendicular ao plano , e que passa pelo ponto O distante do centro do disco. O disco não encosta na parede e, portanto, não há atrito com a parede vertical. Inicialmente, o centro de massa está na altura do eixo de rotação e um pequeno pino impede o disco de girar. O módulo do vetor aceleração angular do disco no instante em que o pino é removido, em , é:

16. Uma polia homogênea, que possui o formato de um disco com raio e massa , está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O módulo do vetor aceleração de queda do bloco, em , vale aproximadamente:

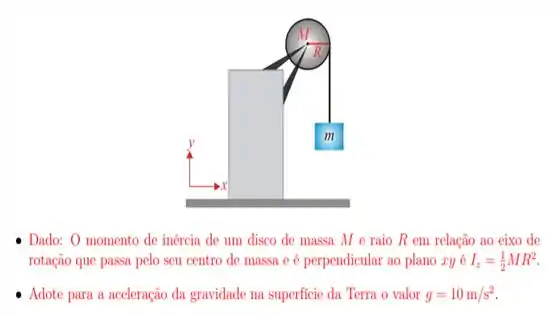
17. Uma polia homogênea, que possui o formato de um disco com raio e massa está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa , como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O sistema é solto do repouso, quando m está a uma altura acima do chão horizontal. O módulo do vetor velocidade com que o bloco de massa m chega ao chão, em metros por segundo, é aproximadamente:

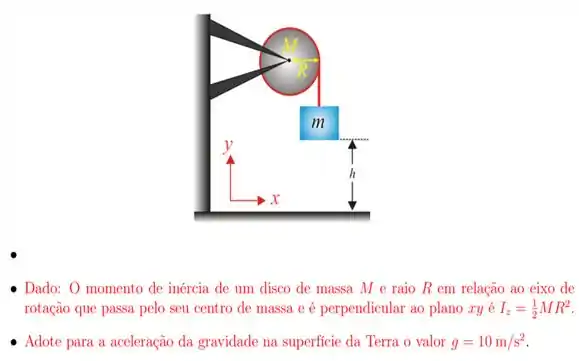
18. O sistema mostrado na figura é formado por duas partículas de massas iguais fixadas às extremidades de uma haste de massa desprezível e com comprimento . O sistema pode girar livremente, sem atrito, em um plano horizontal com velocidade angular em torno de um eixo fixo vertical que passa pelo centro de massa do sistema. Subitamente, um gás comprimido que está no interior da haste a expande até um comprimento de . Diante disso, o módulo do vetor velocidade angular, em radianos por segundo, que o sistema adquire após a expansão é:

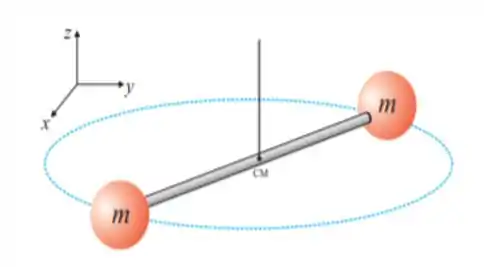
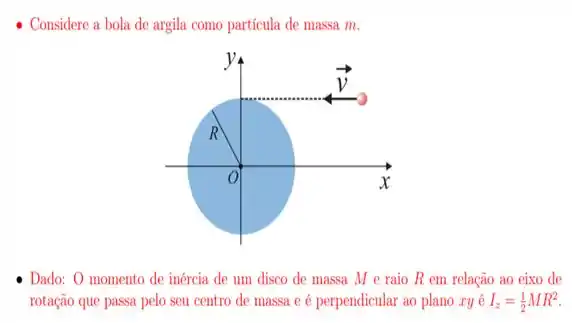
19. Uma bola de argila com massa é arremessada com velocidade ) tangencialmente à borda de um disco homogêneo de massa e raio . O disco repousa sobre uma superfície lisa (no plano ) e pode girar sem atrito em torno de um eixo fixo, que passa pelo centro do disco (o ponto da figura) e que está orientado na direção do eixo . Considerando que, ao colidir com a borda do disco, a argila gruda-se a ela, podemos afirmar que o módulo da velocidade angular do disco, em radianos por segundo, após a colisão é:

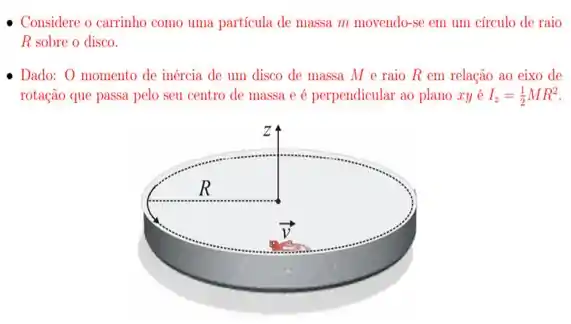
20. Um carrinho de brinquedo, de massa , move-se no sentido anti-horário na borda de um disco horizontal de forma circular, com raio e massa . Esse disco pode girar livremente, sem atrito, em torno de um eixo vertical fixo que passa pelo seu centro. Inicialmente, a velocidade escalar do carrinho (em relação ao chão) é , e o disco gira no sentido horário com velocidade angular em módulo igual a . Em dado instante, o carrinho para de se mover sobre o disco. O módulo do vetor velocidade angular do disco, em radianos por segundo, depois que o carrinho para é:

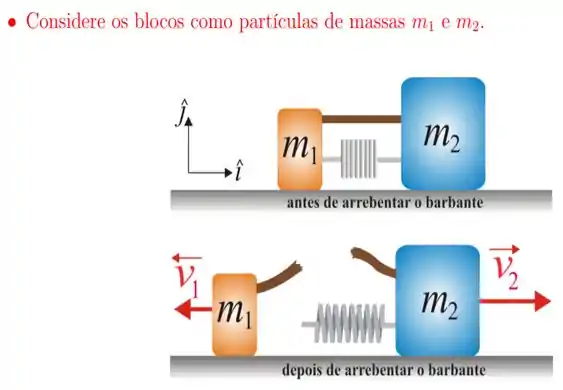
10. Dois blocos de massas e estão parados sobre uma superfície horizontal sem atrito. Uma mola leve (de massa desprezível), comprimida, é presa a um dos blocos. Um barbante que inicialmente mantém os blocos juntos arrebenta-se; depois disso, o bloco de massa move-se com velocidade , e o bloco de massa move-se com velocidade . A energia potencial elástica antes do barbante arrebentar, em Joules, é:

6. Um pequeno drone está navegando numa dada altura constante quando, por causa de um defeito de fabricação, explode em dois fragmentos. Imediatamente após a explosão, verifica-se que um dos fragmentos com massa , move-se com velocidade e o outro fragmento, de massa , move-se com velocidade , ambas velocidades medidas no mesmo referencial inercial em repouso. A velocidade escalar do drone antes da explosão, em metros por segundo, medida no mesmo referencial inercial é: