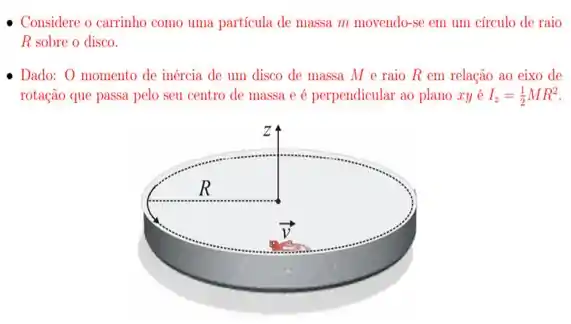
20. Um carrinho de brinquedo, de massa , move-se no sentido anti-horário na borda de um disco horizontal de forma circular, com raio e massa . Esse disco pode girar livremente, sem atrito, em torno de um eixo vertical fixo que passa pelo seu centro. Inicialmente, a velocidade escalar do carrinho (em relação ao chão) é , e o disco gira no sentido horário com velocidade angular em módulo igual a . Em dado instante, o carrinho para de se mover sobre o disco. O módulo do vetor velocidade angular do disco, em radianos por segundo, depois que o carrinho para é:
Passo 1
E aí meus caros! Esse é o momento pelo qual tanto esperávamos! Aqui vamos nós pra última questão dessa de Física!
A questão nos diz que um carrinho começa a mover-se no sentido anti-horário na borda de um disco que está girando em torno de um eixo. Até que em determinado instante o carrinho para de se movimentar em relação ao disco. E a questão, então, nos pede a velocidade do sistema formado pelos dois corpos nesse instante
Bom! Pelo que podemos ver, trata-se provavelmente de uma questão sobre conservação de momento angular. Cuidado que não se pode afirmar isso sem, ao menos ver se tem alguma força ou torque externo agindo no sistema.
Sem mais delongas, vamos começar nossa resolução fazendo o diagrama de corpo livre pro nosso sistema, definindo as coordenadas e tal...
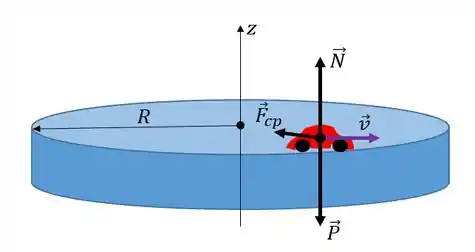
Há duas forças atuando sobre o carrinho, que são a força peso e a força de reação normal do disco. Em relação ao ponto central do disco, por onde passa o eixo de rotação, não existem torques externos devido às forças peso e normal se anularem.
A força centrípeta que atua no carrinho é radial e não causa torque em relação ao eixo de rotação. A alteração da velocidade do carrinho ocorre devido a força de contato entre o disco e o carrinho.
Todas essas forças são internas ao sistema. Elas alteram o módulo da velocidade do carrinho e do disco. Elas causam torque tanto no disco quanto no carrinho, embora o torque resultante no sistema (disco + carrinho) seja nulo.
Desse modo, como o torque resultante no sistema durante todo o tempo é nulo, o momento angular do sistema se conserva.
Passo 2
Se liga! Inicialmente tanto o disco como o carrinho estão em movimento. Sendo assim, o momento angular do sistema (disco + carrinho) será dado por:
Onde o momento angular do carrinho, que gira em sentido anti-horário em torno do disco de raio , é dado por:
E o momento angular do disco, que gira em sentido horário, é dado por:
Onde e são o momento de inércia e o vetor velocidade angular do disco. No caso, o sinal negativo aí vem do fato dos dois objetos estarem girando em sentidos opostos. Geralmente se adota o sentido horário como o negativo.
Ficamos então, com...
Passo 3
Em dado instante o carrinho para de se movimentar em relação ao disco. Nesta condição, o carrinho passa a movimentar-se com a mesma velocidade angular que o disco. O momento angular final do sistema, será então, dado por:
Já sabemos que o momento de inércia do disco é:
Quanto ao momento de inércia do carrinho, pelo teorema dos eixos paralelos, temos que:
Sendo assim, obtemos que...
Passo 4
Agora, é só uma questão de igualar os momentos angulares final e inicial:
Isolando :
A questão pede pra gente o módulo de . Façamos isso...
Substituindo os valores numéricos que nós temos:
Finalmente chegamos à nossa resposta!
Essa é a velocidade angular final do sistema (carrinho+disco).
Ufa!!! Terminamos aqui! It’s a long exam!!!