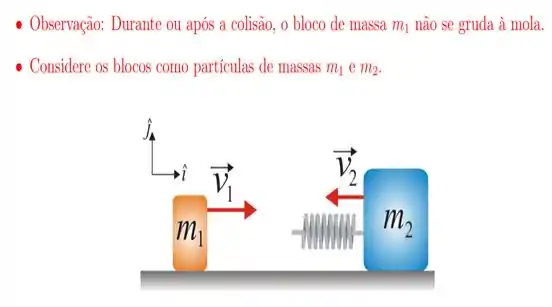
11. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível) conectada a um bloco de massa , que se move com velocidade . Durante o processo de colisão, quando a velocidade do bloco é , a energia potencial elástica armazenada na mola é:
Passo 1
E aí galerinha! Aqui, vamos nós pra décima primeira questão dessa maravilhosa de Física.
E temos aqui, mais uma questãozinha sobre momento!
Já sabe, né!? Antes de qualquer coisa, pra resolver esse tipo de questão temos que pôr os pingos nos issss! Esses são os diagramas de força e momentos atuantes nos dois blocos, antes da colisão:
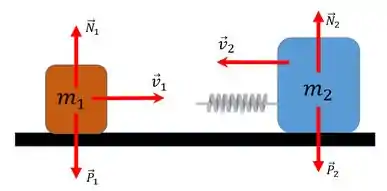
Se liga só nisso! A força externa resultante no sistema (devido à soma vetorial da força da gravidade e da força normal em cada um dos bloco) é nula, afinal o bloco não sai voando por aí né!? Sendo assim, durante a colisão atuam apenas forças internas ao sistema. Pelo que podemos classificá-lo como um sistema bem isolado.
E se falou em sistema isolado, então, podemos utilizar a conservação do momento linear do sistema durante todo o processo de colisão e com isso determinar a velocidade do bloco de massa quando a velocidade do bloco é .
Passo 2
Pois vamos lá! Apliquemos a conservação do momento linear:
Isolando a velocidade final do bloco de massa , que é o que estamos procurando:
Passo 3
Passo 4
Tá lembrado lá que o produtor falou que o nosso sistema é isolado!
Pois bem! Se o sistema é bem isolado, quer dizer que além do momento linear, a energia também se conserva!
A energia potencial elástica pode ser determinada por conservação da energia mecânica do sistema uma vez que a força da mola é uma força conservativa.
Antes da colisão, o único tipo de energia presente era a cinética. Depois da colisão, além da energia cinética, teremos também a presença de energia potencial elástica.
Sendo assim, vamos ajustar a equação de energia, que vai ficar com a seguinte cara:
Passo 5
Agora, vamos determinar o valor de através da fórmula abaixo:
Do enunciado, sabemos que:
E então, substituindo esses valores acima, chegamos ao seguinte resultado para :
Em módulo:
Com isso, temos que a energia potencial elástica será igual à:
Pronto! Missão cumprida!
Terminamos aqui!
Bora pra próxima!