17. Uma polia homogênea, que possui o formato de um disco com raio e massa está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa , como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O sistema é solto do repouso, quando m está a uma altura acima do chão horizontal. O módulo do vetor velocidade com que o bloco de massa m chega ao chão, em metros por segundo, é aproximadamente:
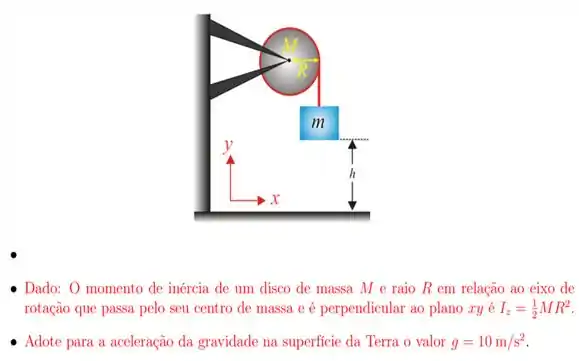
Passo 1
E aí meus caros! Aqui vamos nós pra décima sétima questão dessa de Física!
E assim como no item anterior, temos aqui uma questão de polia com massa suspendendo um bloco. Uma questão de rotação, pra ser mais direto.
E em questões de rotação, como já falamos antes, o negócio é o seguinte. Quase sempre se resolve por análise de forças ou energia ou até mesmo os dois juntos.
Depende muito do que o enunciado fala pra gente. É o enunciado que nos dá as pistas de como vamos resolver o problema!
Pois muito bem! O que a questão tá pedindo pra gente é pra determinar a velocidade do bloco de massa , quando ele é solto do repouso de uma altura . Sei não, hein!? Se a questão deu uma altura pra gente isso tá cheirando à conservação de energia mecânica! Ainda mais, porque não tem atrito agindo em nosso sistema!
Sendo assim não há mais o que discutir! Como é de costume! A primeira coisa que temos de fazer é o diagrama de corpo livre do nosso sisteminha...
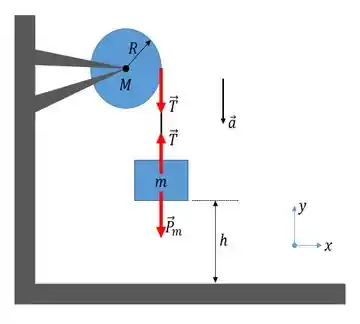
Passo 2
Bem! Como já discutido antes, vamos obter a solução utilizando a conservação da energia mecânica do sistema uma vez que os movimentos do cilindro e do bloco ocorrem na ausência de forças de atrito.
Se liga! Toda a energia potencial do bloco será transformada em energia cinética de rotação do disco mais a energia cinética de translação do bloco, que terá energia potencial nula ao chegar em . Assim, com base nisso, podemos escrever a seguinte equação:
Onde é a velocidade angular do cilindro, é a velocidade de translação do bloco no instante em que ele chega no plano e é o momento de inércia do disco.
Sabendo que a velocidade de translação do bloco é igual a velocidade linear do disco, que no caso é dada por:
Substituindo essa relação na equação anterior:
E sabendo também que:
Então;
Passo 3
Agora, é só substituir os valores numéricos conhecidos de cada variável:
E pronto! Encontramos a velocidade do bloco após ser solto de uma altura de .
Hasta lá vista!
Bora pra frente! Faltam só mais três questões!