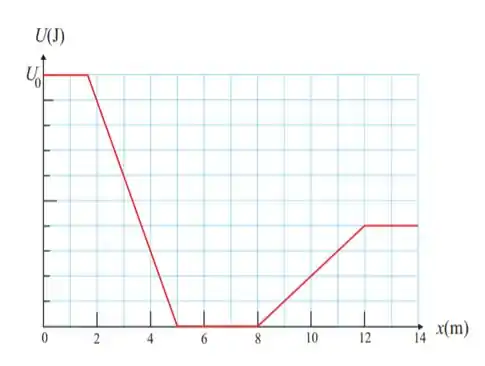
9. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial representada na figura abaixo onde a escala no eixo é definida por . Se a partícula é liberada em com energia , a sua velocidade escalar, em , na posição , é:
Passo 1
E aí galerinha! Aqui, vamos nós pra nona questão dessa maravilhosa de Física.
E mais uma vez, temos aqui um problema sobre energia, dessa vez, envolvendo a análise e interpretação de gráficos.
Se liga só! Temos um gráfico de energia potencial em função da posição da partícula.
E também sabemos que a partícula está sujeita a uma única força conservativa, que é justamente a força que dá origem ao gráfico.
Além disso, temos que ao longo da trajetória da partícula, sua energia mecânica pode ser dada pela soma da energia potencial com a energia cinética . Do seguinte modo:
Agora, vamos olhar direitinho o nosso gráfico. Se liga naquela parte do gráfico entre e . Viu alguma coisa de diferente ali?
É isso mesmo amiguinho(a)! Aquela zona ali é uma região especial do nosso gráfico! Nela a energia potencial vale zero! Ou seja, quer dizer que toda energia mecânica nessa parte está concentrada na forma de energia cinética.
Sendo assim, tomando a energia cinética da partícula na posição onde ela é liberada, , esta vai ser a energia mecânica total da partícula, pois sua energia potencial é nula. E esta energia vai ser dada por:
Passo 2
Agora na posição ... As coisas vão ser um pouco diferentes. Podemos ver pelo gráfico, que a energia potencial nessa configuração vai ser igual a . Como esse valor é menor que a energia mecânica em ; então a partícula também vai ter uma energia cinética. De modo que sua energia mecânica total será:
Igualando as duas energias mecânicas:
E isolando :
Substituindo os valores dados de e :
E pronto! Encontramos a velocidade da partícula quando ela está na posição .
Bora pra próxima!