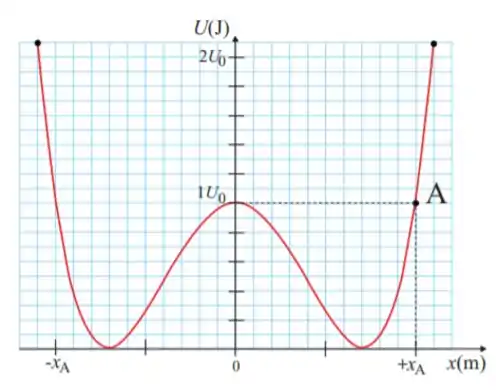
8. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial mostrada no gráfico abaixo. Se a partícula passa pelo ponto A de coordenada com velocidade escalar , a sua velocidade escalar quando passa por um ponto de equilíbrio estável, em metros por segundo, é aproximadamente:
Passo 1
E aí meus caros! Aqui, vamos nós resolver mais um probleminha dessa maravilhosa prova de Física.
E mais uma vez, temos aqui um problema sobre energia, dessa vez, envolvendo a análise e interpretação de gráficos.
Se liga só! Temos um gráfico de energia potencial em função da posição da partícula.
E também sabemos que a partícula está sujeita a uma única força conservativa, que é justamente a força que dá origem ao gráfico.
Assim, pegando por exemplo o ponto , isso significa que em qualquer trecho da trajetória da partícula, a energia mecânica total do sistema será igual a energia no ponto , que é dada por:
Mas o que a questão quer da gente, é a velocidade da partícula ao passar por um ponto de equilíbrio estável!
E o quê que é isso produtor!? Como relacionar isso com o gráfico do enunciado?
Presta atenção! Num ponto de equilíbrio estável, a energia potencial tem um mínimo local. A resposta do sistema a pequenas perturbações ou uma distância arbitrariamente pequeno do ponto de equilíbrio é de volta ou oscilar em torno do ponto de equilíbrio. Em linhas gerais, são aqueles pontos no nosso gráfico do enunciado, onde a energia potencial é igual a zero.
Esses pontos aqui embaixo! Tá ligado!
Passo 2
E se a energia potencial nesses pontos de equilíbrio estável vale zero, isso significa que nessa posição, a partícula só possui energia cinética, estando com uma velocidade , que é a que procuramos.
Desse modo, igualando a energia no ponto com a do ponto de equilíbrio estável:
E isolando :
Essa é a expressão que procurávamos! Já temos o valor de e de . Falta apenas descobrir quanto vale !
Acredito que esse tenha sido o problema da questão! Pois bem! Se liga só! Cada tracinho no eixo das ordenadas equivale a . Sendo assim, o valor de será de
Pronto! Temos tudo que precisávamos! O valor de então, vai ser igual à: