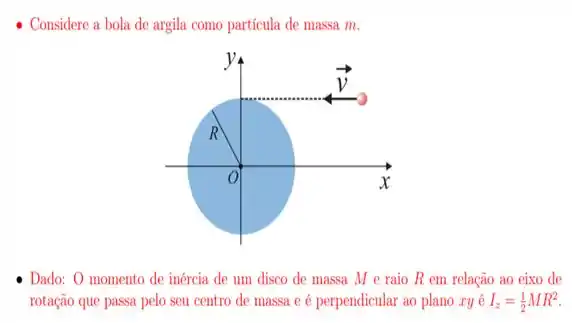
19. Uma bola de argila com massa é arremessada com velocidade ) tangencialmente à borda de um disco homogêneo de massa e raio . O disco repousa sobre uma superfície lisa (no plano ) e pode girar sem atrito em torno de um eixo fixo, que passa pelo centro do disco (o ponto da figura) e que está orientado na direção do eixo . Considerando que, ao colidir com a borda do disco, a argila gruda-se a ela, podemos afirmar que o módulo da velocidade angular do disco, em radianos por segundo, após a colisão é:
Passo 1
E aí meus caros! Aqui vamos nós pra penúltima questão dessa de Física!
A questão nos diz que uma bolinha de argila é arremessada com uma certa velocidade e vai colidir tangencialmente na borda de um disco preso a um eixo. Após a colisão, a argila gruda-se ao disco e o sistema passa a girar
Bom! Pelo que podemos ver, tem tudo pra ser uma questão sobre conservação de momento angular.
E como é quase uma tradição, vamos começar nossa resolução fazendo o diagrama de corpo livre pro nosso sistema, definindo as coordenadas e tal...
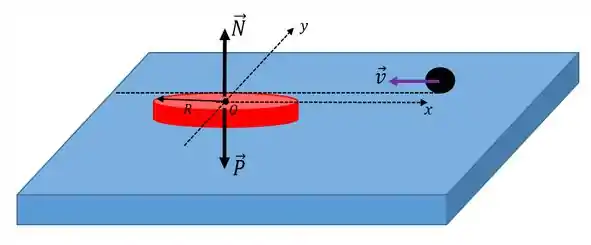
Há duas forças atuando sobre o disco, que são a força peso do disco e a força de reação normal do plano. Em relação ao ponto central do disco, não existem torques externos (devido às forças peso e normal se anularem) sobre o sistema (disco com argila), de modo que o momento angular do mesmo deve se conservar em relação ao ponto O.
Como não tem torque externo, então o momento angular do nosso sistema se conserva!
Passo 2
Se liga! O momento angular inicial é devido apenas ao movimento da argila. O disco em repouso não possui momento angular inicial.
Para o movimento da argila no plano , o momento angular da argila em relação ao ponto O é dado por:
E é importante destacar que esse momento é constante enquanto se aproxima do disco, pois não existe torque exercido sobre a argila até que ela colida com o disco.
Durante a colisão, aparecem forças tanto na argila como no disco, que alteram a condição de movimento tanto da argila (que tem a sua velocidade reduzida) quando do disco (que passa a rodar). Entretanto, essas são forças internas ao sistema formado por (disco+argila) e por isso o momento angular do sistema se conserva. O problema seria se essas fossem forças externas.
Após a colisão inelástica, o momento angular final é dado por:
Onde o momento angular da argila é dado por:
E o momento angular do disco, depende do seu momento de inércia e é dado por:
Mas tem uma coisa interessante aqui! A questão fala pra gente que a argila fica presa no disco. Portanto, os dois passam a ter a mesma velocidade... Sendo assim, pode ser escrita como:
E então, temos que:
Passo 3
Como já sabemos que o momento se conserva...
Igualando os módulos dos dois:
E isolando :
Substituindo os valores numéricos já conhecidos, o módulo deles viu!?
Obtemos a velocidade angular do sistema (disco+argila) após a colisão!
Faltam só mais uma galera!
Bora pra frente!