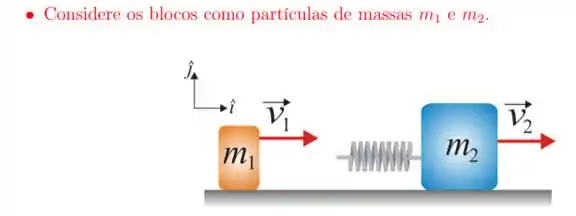
12. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível), de constante elástica , conectada a um bloco de massa , que se move com velocidade . Sabe-se que na máxima compressão da mola , os blocos têm a mesma velocidade. O valor da máxima compressão da mola, em centímetros, é dada por:
Passo 1
A moda agora é a questão 12, galerinha!
Mais uma questãozinha sobre momento aí pra gente resolver!
E essa questãozinha é quase igual às questões 10 e 11, que já tratamos de resolver. A única diferença é o sentido das velocidades antes da colisão.
Das questões anteriores, a gente sabe que a força externa resultante no sistema (devido à soma vetorial da força da gravidade e da força normal em cada um dos bloco) é nula, afinal o bloco não sai voando por aí né!? Sendo assim, durante a colisão atuam apenas forças internas ao sistema. Pelo que podemos classificá-lo como um sistema bem isolado.
E se falou em sistema isolado, então, podemos utilizar a conservação do momento linear do sistema durante todo o processo de colisão e com isso determinar a velocidade do sistema depois da colisão, já que as massa ficam unidas pela mola.
Passo 2
Pois vamos lá! Apliquemos a conservação do momento linear:
Isolando a velocidade final do sistema formado pelos dois blocos, que é o que estamos procurando:
Passo 3
E do exercício anterior, também sabemos que se o sistema é bem isolado, quer dizer que além do momento linear, a energia também se conserva!
A máxima compressão da mola pode ser determinada por conservação da energia mecânica do sistema uma vez que a força da mola é uma força conservativa.
Antes da colisão, o único tipo de energia presente era a cinética. Depois da colisão, além da energia cinética resultante da união dos dois blocos, teremos também a presença de energia potencial elástica, que é devido a compressão da mola quando os blocos ficam quase grudados.
Sendo assim, vamos ajustar a equação de energia, que vai ficar com a seguinte cara:
Passo 4
Agora, vamos determinar o valor de através da fórmula abaixo:
Do enunciado, sabemos que:
E então, substituindo esses valores acima, chegamos ao seguinte resultado para :
Com isso, temos que a compressão da mola será igual à:
Pronto! Missão cumprida!
Terminamos aqui!
Bora pra próxima!