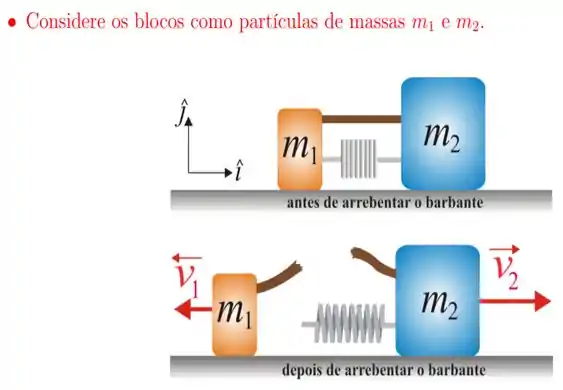
10. Dois blocos de massas e estão parados sobre uma superfície horizontal sem atrito. Uma mola leve (de massa desprezível), comprimida, é presa a um dos blocos. Um barbante que inicialmente mantém os blocos juntos arrebenta-se; depois disso, o bloco de massa move-se com velocidade , e o bloco de massa move-se com velocidade . A energia potencial elástica antes do barbante arrebentar, em Joules, é:
Passo 1
E aí galerinha! Aqui, vamos nós pra décima questão dessa maravilhosa de Física.
E temos aqui, uma questãozinha sobre momento!
Antes de qualquer coisa, pra resolver esse tipo de questão temos que pôr os pingos nos isss! Esses são os diagramas de força e momentos atuantes nos dois blocos:
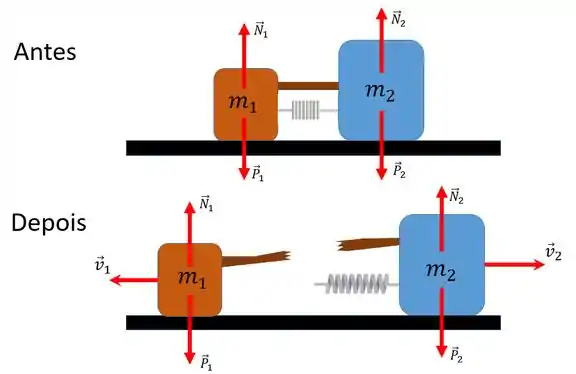
Se liga só nisso! A força externa resultante no sistema (devido à soma vetorial da força da gravidade e da força normal em cada um dos bloco) é nula, afinal o bloco não sai voando por aí né!? Sendo assim, durante a colisão atuam apenas forças internas ao sistema. Pelo que podemos classificá-lo como um sistema bem isolado.
E se falou em sistema isolado, então, podemos utilizar a conservação do momento linear do sistema durante todo o processo de colisão e com isso determinar com que velocidade o bloco de massa sai da colisão.
Passo 2
Pois vamos lá! Apliquemos a conservação do momento linear:
Presta atenção! Os blocos estavam parados antes da colisão. Logo, não tinha velocidade nenhuma aí, e então o momento do sistema será nulo...
Olhando a figura do enunciado, temos que:
Isolando a velocidade do bloco de massa , que é :
Passo 3
Ah! Mas a gente só isolou o !? E agora? Como é que a gente vai fazer pra obter o valor dele?
Lembra lá que o produtor falou que o nosso sistema é bem isolado!?
Ora bolas! Se o sistema é bem isolado, quer dizer que além do momento linear, a energia também se conserva!
A força da mola é uma força conservativa e, após a colisão, a energia potencial elástica armazenada inicialmente na mola vai ser transformada integralmente em energia cinética do sistema. Sendo assim, vamos ajustar a equação, que vai ficar com a seguinte cara:
A velocidade nós já temos! Falta só a velocidade ! Pois bem! Ela é dada por:
E então, temos que a energia potencial elástica antes do barbante arrebentar vai ser igual à:
Pronto! Finalizamos aqui!
Bora pra próxima!