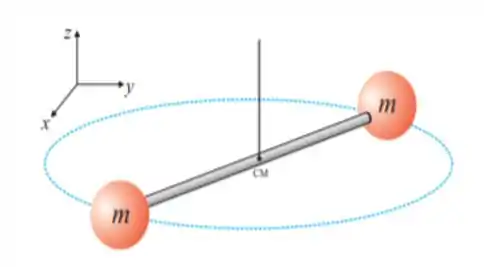
18. O sistema mostrado na figura é formado por duas partículas de massas iguais fixadas às extremidades de uma haste de massa desprezível e com comprimento . O sistema pode girar livremente, sem atrito, em um plano horizontal com velocidade angular em torno de um eixo fixo vertical que passa pelo centro de massa do sistema. Subitamente, um gás comprimido que está no interior da haste a expande até um comprimento de . Diante disso, o módulo do vetor velocidade angular, em radianos por segundo, que o sistema adquire após a expansão é:
Passo 1
E aí meus caros! Aqui vamos nós pra décima oitava questão dessa de Física!
A questão nos mostra um sistema formador por duas partículas de massas iguais fixadas às extremidades de uma haste de massa desprezível, que está girando.
Rapaz! Sei não, hein!? Isso tá cheirando a questão sobre conservação de momento angular!
Bom! Como é quase uma tradição, vamos começar nossa resolução fazendo o diagrama de corpo livre pro nosso sistema, definindo as coordenas e tal...
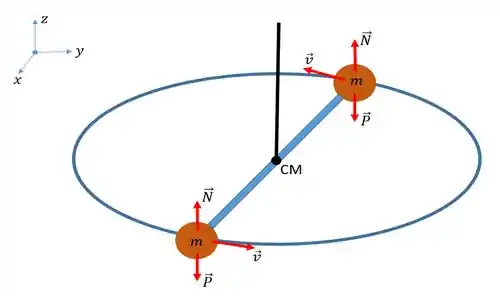
Consideraremos o sistema de coordenadas com origem no CM. As forças externas exercidas nas partículas são a força normal do contato com o plano horizontal e a força gravitacional que a Terra exerce em cada uma das partículas. Essas forças dão um torque resultante nulo no sistema em relação ao centro de massa do sistema (por simetria).
Durante a expansão, as forças empurram para fora do eixo (forças radiais) e não exercem torque algum em relação ao CM. Portanto o momento angular do sistema é conservado em relação ao CM.
Os vetores momenta angulares antes e depois da expansão, e , respectivamente, são perpendiculares ao plano de movimento. De acordo com a imagem abaixo;
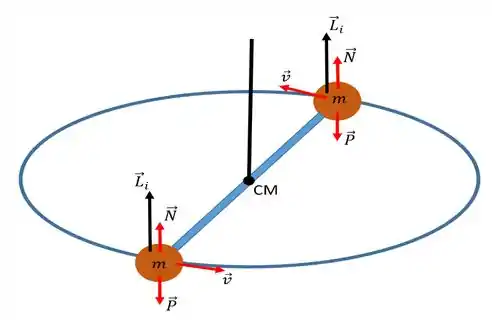
E as partículas movem-se em círculos, de modo que cada uma possui um momentum angular da forma...
Uma vez que :
Da figura, podemos ver que é metade do comprimento da haste. Sendo assim...
Passo 2
Como as duas massas são iguais e estão a uma mesma distância do centro de massa, então elas têm o mesmo momento angular. Assim, o vetor momento angular inicial do sistema é:
Isso é quando o comprimento inicial da haste é de . Após a expansão, como as massas são iguais e estão também a uma mesma distância do centro de massa, o momento angular final da haste será de:
Sendo assim, como não há nenhum torque externo agindo sobre nosso sistema, então o momento angular dele é conservado...
Passo 3
Igualando os módulos dos dois momentos:
E substituindo os valores numéricos já conhecidos:
Obtemos a velocidade angular final do sistema após a expansão!
Faltam só mais duas galera!
Bora pra frente!