16. Uma polia homogênea, que possui o formato de um disco com raio e massa , está fixa em um suporte podendo girar livremente, sem atrito, em volta de um eixo que passa pelo seu centro e é perpendicular ao plano . Uma corda leve (de massa desprezível), que está enrolada nessa polia, prende um bloco de massa como mostra a figura. À medida que a polia gira, o bloco se movimenta para baixo, sem que a corda escorregue sobre a polia. O módulo do vetor aceleração de queda do bloco, em , vale aproximadamente:
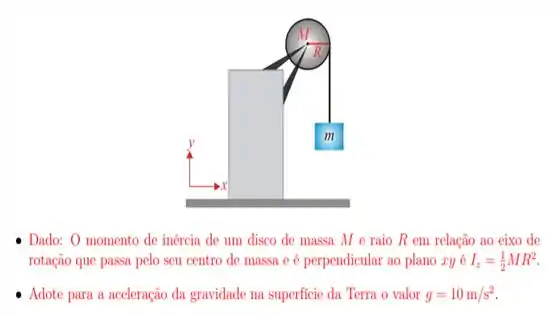
Passo 1
E aí meus caros! Aqui vamos nós pra décima sexta questão dessa de Física!
O que a gente tem aqui é clássica questão de polia com massa suspendendo um bloco. Uma questão de rotação, pra ser mais direto.
E em questões de rotação, o negócio é o seguinte. Quase sempre se resolve por análise de forças ou energia ou até mesmo os dois juntos.
O que a questão tá pedindo pra gente é pra determinar a aceleração desse bloquinhos. Sei não, hein!? Isso tá cheirando à segunda lei de Newton! Bom! Como é de costume! A primeira coisa que temos de fazer é o diagrama de corpo livre do nosso sisteminha...
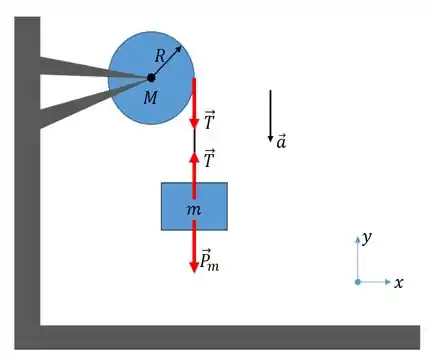
Passo 2
Bem! Temos duas forças agindo sobre o bloco, a força peso e a força de tração da corda de massa desprezível. Se o nosso bloco vai ser acelerado graças a essas duas forças, apliquemos então, a Lei de Newton para ele:
Agora lembra lá que o produtor falou que a polia tem massa! Isso quer dizer que a gente também que ela também vai estar sujeita à tração da corda. Por isso, usemos a segunda lei de Newton para objetos sujeitos a rotação...
Do enunciado sabemos que o momento de inércia é dado por:
E sabendo que, uma vez que a corda não desliza, a aceleração angular é dada por:
Isolando então, a tração :
Passo 3
Finalmente chegamos a relação que queríamos para . Agora é só substituir ela na equação abaixo...
E encontramos o valor de em função das variáveis dadas. Como massa só tem valor positivo, isso aí já tá em módulo, ok?
Hasta la vista!
Terminamos aqui! Bora pra frente que atrás vem gente!