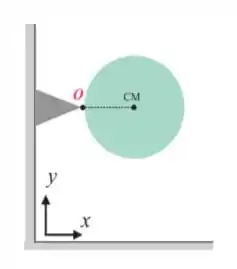
13. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor aceleração angular do disco no instante em que ele é abandonado, em , é:

Passo 1
E aí galerinha! Olha nós aqui de novo!
E dessa vez, temos uma questãozinha um tanto peculiar pra resolver... Um misto de rotação com torque com força... É uma questãozinha pra ninguém botar defeito!
É por isso mesmo, que nesse tipo de questão a primeira coisa que a gente tem de fazer é o diagrama de corpo livre do nosso sisteminha, no caso o disco. Bora lá!
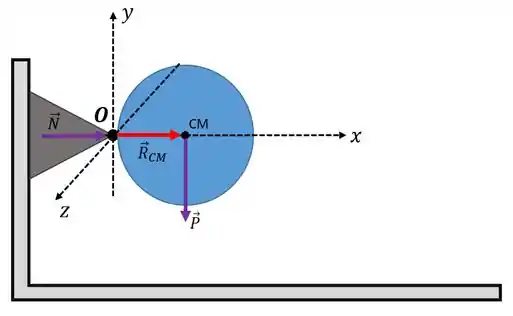
Temos duas forças agindo sobre o nosso disco, que são a força peso (uma vez que ele tem massa) e a força normal que o pivô exerce sobre o disco.
Repara que a gente até fez um sistema de coordenadas tridimensional ali no esboço... Tudo pra facilitar o entendimento, hein!?
Agora se liga! é o ponto onde o disco se prende ao pivô. É o ponto por onde passa o eixo que conecta o pivô ao disco. E é também o ponto mais importante aqui pra nossa análise. Sabe por quê?
Ora bolas! Olha de novo a figura que fizemos! Presta atenção na localização da força peso! A força responsável por dar o torque no disco é a força peso, que age no seu centro de massa. Sendo assim, pela imagem temos que:
O que estamos fazendo aí, é o produto vetorial entre os vetores e sendo o vetor que indica o ponto de aplicação da força peso em relação ao ponto . Viu o porquê da importância de termos feito um sistema de coordenas, além é claro dos professores aí na universidade serem bem rigorosos com isso.
Assim, pelo nosso sistema de coordenadas, o produto vetorial de antes vai ficar assim:
Passo 2
Bem! E sabemos que se um torque está sendo gerado ao longo do nosso disco, então ele vai começar a girar, né não!? Ele começa a girar, adquirindo uma aceleração angular . Além disso, como nosso disco tem massa, e por conseguinte momento de inércia , em uma rotação de corpo rígido temos que:
Tirando o módulo, ou seja, deixando em valor absoluto:
A próxima coisa a se fazer é determinar o momento de inércia do disco. Pois bem! Pelo teorema dos eixos paralelos:
Uma vez que o momento de inércia passando pelo centro de massa de um disco é:
E olhando a figura do , chegamos ao seguinte valor para :
O módulo da aceleração angular vai ser igual à:
Substituindo os valores numéricos dados:
Chegamos ao valor que tanto procurávamos!
Bora pra próxima!