Halliday - Vol.1 - Ed. 8 - Capítulo 3 – Seção 6 – Questão 8
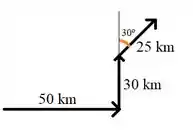
(Capítulo 3.6 – Exercício 8) Um carro viaja para leste, para o norte e em uma direção a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relação ao ponto de partida.
Passo 1
Faalaa galerinha, vamos lá! Aqui temos o trajeto de um carro, e aí queremos encontrar:
- O módulo
- O ângulo do deslocamento em relação ao ponto de partida
Inicialmente vamos ilustrar o deslocamento num diagrama vetorial para facilitar a visualização.
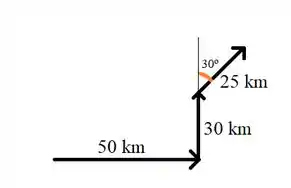
Passo 2
a) Para determinarmos o módulo do vetor deslocamento faremos um somatório vetorial, no qual consideraremos norte como o sentido positivo de e o sentido leste como o sentido positivo de , assim decompondo os vetores em componentes:
Agora, somando as componentes dos vetores:
Passo 3
Com o vetor soma em mãos, utilizaremos a definição de módulo do vetor:
Então:
Passo 4
b) Usando o mesmo referencial utilizado no passo 2, podemos calcular o ângulo montando um triângulo retângulo com as componentes do vetor e o vetor:
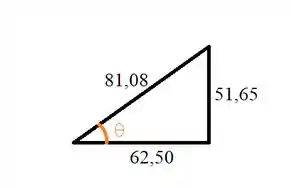
Aplicando a definição de cosseno:
Isolando :
Portanto, o vetor deslocamento do carro está a do semieixo positivo, show?
