Halliday - Vol.1 - Ed. 8 - Capítulo 3 – Seção 6 – Questão 11
(Capítulo 3.6 – Exercício 11) Uma pessoa deseja chegar a um ponto que está a de sua localização atual, em uma direção ao norte do leste. As ruas por onde pode passar são todas na direção norte-sul ou na direção leste-oeste. Qual é a menor distância que a pessoa precisa percorer para chegar ao destino?
Passo 1
E aíí gente, vamos lá ajudar a pessoa a caminhar menos utilizando vetores?? :P
Inicialmente vamos fazer a representação do vetor deslocamento no plano cartesiano. Como a pessoa quer ir em uma direção ao norte do leste, teremos algo desse tipo:
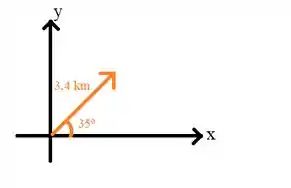
No plano, representamos a reta que é a menor distância entre dois pontos. Considerando o eixo positivo apontando para o norte como pedido no problema, o deslocamento não pode ser feito através dessa reta, pois o enunciado pede apenas distâncias verticais e horizontais.
Tá... mas então como encontramos a menor distância dentro das indicações dadas no enunciado?
É o que veremos agora!!!
Passo 2
Chamaremos o vetor ilustrado acima de Como ele é a menor distância, considerando que o enunciado pede apenas distâncias verticais e horizontais, a menor distância nessa modalidade será a soma das componentes desse vetor. Ou seja, iremos decompor o vetor :
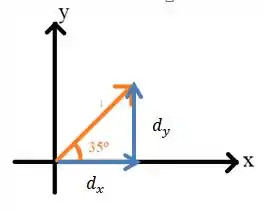
Substituindo os vetores apresentados no enunciado:
Passo 3
Beleza! Temos os valores para e , mas queremos encontrar uma distância total mínima.
E agora?!
Calma, meu pequeno gafanhoto!!
Não importa se essa pessoa for andando totalmente para o Leste e depois para o Norte, ou se ela for ziguezagueando, a distância percorrida vai dar na mesma, afinal, ela só pode caminhar na direção vertical ou horizontal.
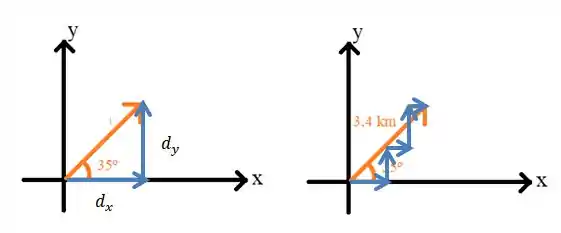
Nesses dois movimentos aí em cima, a distância percorrida vai ser a mesma. É como se todas as setas para a direita somadas vão dar igual ao e todas as setas para cima somadas vão dar igual ao .
Então, para encontrar a distância mínima, basta somarmos esses dois valores:
Ou seja, a menor distância que a pessoa precisa percorrer para chegar ao destino é de .