Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Componentes de Vetores e Vetores Unitários

Ver Teoria
Exercício 291234567891011121314151617181920212223242526272830313233343536373839404142434445464748495051525354555657585960616263

Enunciado

Halliday - Vol.1 - Ed. 8 - Capítulo 3 – Seção 4 – Questão 6

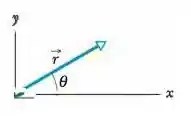
(Capítulo 3.4 – Exercício 6) Um vetor deslocamento r → no plano x y tem 15   m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.

Passo 1

E aíí galera, belezinha? Vamos lá pra mais uma de vetores

Inicialmente vamos fazer a ilustração das componentes no plano x y para visualizar melhor.

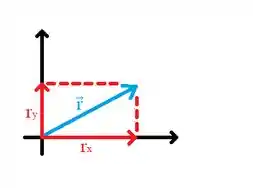
Para determinar as componentes do vetor r → vamos formar com as componentes e o vetor um triângulo retângulo para facilitar a visualização:

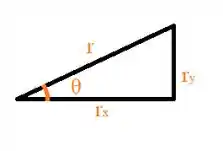
Para determinar as componentes do r → usaremos as relações trigonométricas no triângulo retângulo acima.

Passo 2

Aplicando a definição do seno:

s e n θ = c a t e t o   o p o s t o h i p o t e n u s a = r y r I s o l a n d o   r y :

r y = r × s e n θ

Substituindo os valores dados no enunciado:

r y = 15 × s e n 30 ° = 7,5   m

Passo 3

Aplicando agora a definição do cosseno:

c o s θ = c a t e t o   a d j a c e n t e h i p o t e n u s a = r x r

Isolando r x e substituindo os valores de r e de θ :

r x = 15 × c o s 30 ° = 13   m

E é issoooo

Resposta

  1. r y = 7,5   m
  2. r x = 13   m

Exercícios de Livros Relacionados

Um explorador polar foi surpreendido por urna nevasca, que reduziu a visibilidade a praticamente zero, quando retornava ao acampamento. Para chegar ao acampamento, deveria ter caminhado 5,6k m para o
Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com 1,00m de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a direita;
Um vetor deslocamento r → no plano x y tem 15m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.
Quais são (a) a componente x e (b) a componente y de um vetor a → do plano x y que faz um ângulo de 250 ° no sentido anti-horário com o semieixo x positivo e tem um módulo de 7,3m ?
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano x y . As componentes ( x e y ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: 30,0