Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Componentes de Vetores e Vetores Unitários

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263

Enunciado

Halliday - Vol.1 - Ed. 8 - Capítulo 3 – Seção 6 – Questão 9

(Capítulo 3.6 – Exercício 9)

(a) Determine a soma a → + b → , em termos de vetores unitários, para a → = 4,0   m i ^ + ( 3,0   m ) j ^ e b ^ = - 13,0   m i ^ + ( 7,0   m ) j ^ . Determine (b) o módulo e (c) a orientação de a → + b → .

Passo 1

Faaaala galera! Aqui queremos somar os vetores a = ( 4,3 ) e b = ( - 13,7 ) e depois encontrar algumas informações sobre eles, belezinha?

Para calcular a soma de dois vetores podemos somar diretamente suas componentes de forma que: A → + B → = A x + B X i ^ + A y + B y j ^ + A z + B z k ^

Vamos lá!

Passo 2

a) Para calcular o vetor soma dos vetores a → e b → dado, utilizaremos a definição acima. Assim:

a → = ( 4,3 )

b → = ( - 13,7 )

Então:

s → = a → + b → = 4 - 13,3 + 7 = ( - 9,10 )

Belezinha, já achamos a soma, agora vamos pros próximos itens

Passo 3

b) Por definição, o módulo do vetor é: A = A x 2 + A y 2 + A z 2

Portanto, com o vetor soma calculado no passo anterior, podemos determinar o módulo do vetor pela definição de módulo acima.

  S → = - 9 2 + 10 2 = 81 + 100 = 13,45   m  

Passo 4

c) Fazendo uma representação do vetor no plano cartesiano:

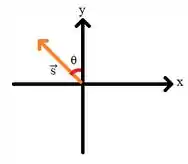
Podemos determinar o ângulo θ fechando um triângulo retângulo com as componentes.

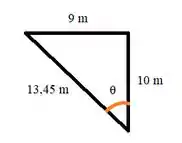
Por definição

c o s θ = c a t e t o a d j a c e n t e h i p o t e n u s a

c o s θ = 10 13,45

Isolando o θ :

θ = arccos ⁡ 10 13,45 = 41,97 °

Portanto, o vetor soma faz um ângulo de 41,9 7 ° com o eixo y positivo.

Arrasamos!

Resposta

  1. a → + b → = 13,45   m
  2. θ = 41,97 ° de norte para oeste

Exercícios de Livros Relacionados

Um explorador polar foi surpreendido por urna nevasca, que reduziu a visibilidade a praticamente zero, quando retornava ao acampamento. Para chegar ao acampamento, deveria ter caminhado 5,6k m para o
Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com 1,00m de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a direita;
Um vetor deslocamento r → no plano x y tem 15m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.
Quais são (a) a componente x e (b) a componente y de um vetor a → do plano x y que faz um ângulo de 250 ° no sentido anti-horário com o semieixo x positivo e tem um módulo de 7,3m ?
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano x y . As componentes ( x e y ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: 30,0