Listas de Estudos pra Prova - Tipler Vol 1 - 6°ed de Física 1 da UTFPR - Leis de Newton

(Cap 4 – Ex 24) Você está sentado em sua cadeira de escritório, com rodinhas, em frente à sua escrivaninha. Considere desprezíveis as forças de atrito entre a cadeira e o chão. No entanto, as forças de atrito entre a cadeira e a escrivaninha são desprezíveis. Quando sentado em repouso, você resolve buscar mais uma xícara de café. Você empurra horizontalmente a escrivaninha e a cadeira rola para trás.

(a) Desenhe o seu próprio diagrama de corpo livre enquanto empurra, indicando claramente qual é a força responsável por sua aceleração.

(b) Qual é a reação à força que provoca sua aceleração?

(c) Desenhe o diagrama de corpo livre da escrivaninha e explique por que ela não acelera. Isto viola a terceira lei de Newton? Explique.

(Cap 4 – Ex 41) Um objeto de 4,0 kg é submetido a duas forças constantes, e . O objeto está em repouso na origem no tempo (a) Qual é a aceleração do objeto?

(b) Qual é a sua velocidade no tempo ?

(c) Onde está o objeto no tempo ?

(Cap 4 – Ex 53) Seu carro atolou na lama. Você está sozinho, mas tem uma corda longa e forte. Tendo estudado física, você amarra a corda fortemente a um poste telefônico e puxa de lado, como mostra a Figura 4-42.

(a) Encontre a força exercida pela corda sobre o carro, quando o ângulo é e você está puxando com uma força de , mas o carro não se move.

(b) Quão forte deve ser a corda se é necessária uma força de para mover o carro quando é

(Cap 4 – Ex 52) Para o sistema das Figuras 4-41a, 4-41b e 4-41c, encontre as massas e as tensões desconhecidas.

(Cap 4 – Ex 49) Na figura 4-38a, um bloco de 0,500 kg está suspenso pelo ponto central de um fio de 1,25 m. As extremidades do fio estão presas ao teto em pontos separados de 1,00 m.

(a) Qual é o ângulo que o fio forma com o teto?

(b) Qual é a tensão no fio?

(c) O bloco de 0,500 kg é removido e dois blocos de 0,250 kg são presos ao fio de forma tal que os comprimentos dos três segmentos do fio são iguais (Figura 4-38b). Qual é a tensão em cada segmento do fio?

(Cap 4 – Ex 50) Uma bola pesando 100 N é mostrada suspensa por um sistema de cordas (Figura 4-39). Quais são as tensões nas três cordas?

(Cap 4 – Ex 57) Uma caixa de está sobre uma rampa sem atrito inclinada de . Alguém puxa a caixa rampa acima com uma corda (Figura 4-44). Se a corda forma um ângulo de com a horizontal, qual é a menor força capaz de deslocar a caixa rampa acima?

(Cap 4 – Ex 70) Duas caixas de são arrastadas sobre uma superfície horizontal sem atrito com uma aceleração constante de , como mostrado na Figura 4-53. Cada corda tem uma massa de . Encontre a magnitude da força e a tensão nas cordas nos pontos A, B e C.

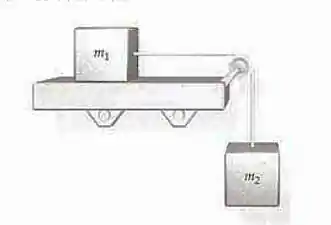
(Cap 4 – Ex 83) Se uma das massas da máquina de Atwood da Figura 4-60 é , quanto deve valer a outra massa de forma a que o deslocamento de cada massa, durante o primeiro segundo após a largada, seja Suponha uma polia sem massa e sem atrito e um fio sem massa.

(Cap 4 – Ex 68) Dois blocos estão em contato sobre uma superfície horizontal sem atrito. Os blocos são acelerados por uma força única horizontal aplicada a um deles (Figura 4-52). Encontre a aceleração e a força de contato do bloco 1 sobre o bloco 2

(a) em termos de F, e , e

(b) para os valores específicos e

(Cap 4 – Ex 82) O aparato da Figura 4-60 é chamado de máquina de Atwood e é usado para medir a aceleração de queda livre medindo-se a aceleração dos dois blocos ligados pelo fio que passa pela polia. Suponha uma polia sem massa e sem atrito e um dio sem massa.

(a) Desenhe o diagrama de corpo livre de cada bloco.

(b) Use os diagramas de corpo livre e as leis de Newton para mostrar que a magnitude da aceleração de cada bloco e que a tensão no fio são e .

(c) Estas expressões fornecem resultados plausíveis se no limite e no limite ? Explique.

(Cap 4 – Ex 67) Uma caixa de massa está sobre uma estante horizontal sem atrito e presas por fios a caixas de massas e , como mostra a Figura 4-51. As duas polias são sem atrito e sem massa. O sistema é largado do repouso. Após a largada, encontre

(a) a aceleração de cada uma das caixas e

(b) a tensão em cada fio.

(Cap 5 – Ex 39) Um bloco de é mantido em repouso contra uma parede vertical por uma força horizontal de .

(a) Qual é a força de atrito exercida pela parede sobre o bloco?

(b) Qual é a força horizontal mínima necessária para evitar que o bloco caia, se o coeficiente de atrito estático entre a parede e o bloco é ?

(Cap 5 – Ex 50) Você e seu melhor amigo fazem uma aposta. Você alega poder colocar uma caixa de encostada a um dos lados de um carrinho, como na figura abaixo, sem que a caixa caia no chão, mesmo você garantindo que não fará uso de ganchos, cordas, prendedores, ímãs, cola ou qualquer outro tipo de adesivo. Quando seu amigo aceita a aposta, você começa a empurrar o carrinho no sentido mostrado na figura. O coeficiente de atrito estático entre a caixa e o carrinho é .

(a) Encontre a menor aceleração com a qual você vencerá a aposta.

(b) Qual é a magnitude da força de atrito, neste caso?

(c) Encontre a força de atrito sobre a caixa se a aceleração é duas vezes a mínima necessária para que a caixa não caia.

(d) Mostre que, para uma caixa de qualquer massa, a caixa não cairá se a magnitude da aceleração para a frente for , onde é o coeficiente de atrito estático.

(Cap 5 – Ex 33) Um bloco de de peso está sobre uma superfície horizontal. Os coeficientes de atrito estático e cinético entre a superfície e o bloco são = 0,80 e = 0,60. Um cordão horizontal é, então, preso ao bloco e uma tensão constante é mantida no cordão. Qual é a magnitude da força de atrito que atua sobre o bloco se (a) , (b) ?

(Cap 5 – Ex 60) Um bloco de está em repouso sobre um suporte de , como mostrado na figura. O suporte de está sobre uma superfície sem atrito. Os coeficientes de atrito entre o bloco de e o suporte sobre o qual ele está apoiado são e .

(a) Qual é a máxima força que pode ser aplicada se o bloco de não deve deslizar no suporte?

(b) Qual é a aceleração correspondente do suporte de ?

(Cap 5 – Ex 3) Um bloco de massa repousa sobre um plano inclinado em um ângulo de com a horizontal. Segue-se que o coeficiente de atrito estática entre o bloco e o plano é

(a)

(b)

(c)

(d) .

(Cap 5 – Ex 62) Um bloco de em um plano inclinado está preso a outro bloco de massa através de uma corda, como nas figuras. Os coeficientes de atrito estático e cinético para o bloco e o plano inclinado são e e o plano é inclinado a com a horizontal.

(a) Determine o intervalo de valores para , a massa do bloco pendurado, para os quais o bloco de não vai se mover a menos que seja perturbado, mas caso seja, vai deslizar para baixo pelo plano inclinado.

(b) Determine um intervalo de valores para para os quais o bloco de não vai se mover a menos que seja perturbado, mas caso seja, vai deslizar para cima pelo plano inclinado.

(Cap 5 – Ex 45) Na Figura abaixo, , e o coeficiente de atrito cinético entre o plano inclinado e o bloco de é . Encontre a magnitude da aceleração das massas e a tensão na corda.

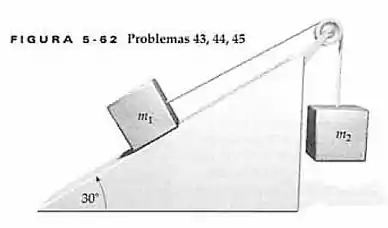
(Cap 5 – Ex 51) Dois blocos ligados por um cordão (figura abaixo) deslizam para baixo sobre um plano inclinado de . O bloco 1 tem a massa e o bloco 2 tem a massa . Ademais, os coeficientes de atrito cinético entre os blocos e o plano são , para o bloco 1 e para o bloco 2. Encontre

(a) a magnitude da aceleração dos blocos e

(b) a tensão no cordão.

(Cap 5 – Ex 43) Um bloco de massa está sobre um plano inclinado de um angulo com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano é . O bloco está amarrado a um segundo bloco de massa que pende livremente de um cordão que passa por uma polia sem massa e sem atrito (Figura abaixo). Depois que o segundo bloco caiu , qual é sua rapidez?

(Cap 5 – Ex 41) APLICAÇÃO EM ENGENHARIA. Você participa de um rali em um dia nevoso, quando a temperatura está próxima do ponto de congelamento. O coeficiente de atrito estático entre os pneus do carro e a estrada congelada é 0,080, O chefe de sua equipe está preocupado com alguns dos morros do percurso e pede para você considerar a troca para pneus de neve. Para resolver a questão ele quer comparar os ângulos dos morros do percurso para ver quais deles seu carro consegue transpor

(a) Qual é o ângulo de inclinação máxima que um veículo com tração nas quatro rodas pode subir com rapidez constante?

(b) Se os morros estão congelados, qual é o ângulo de inclinação máxima para que o mesmo veículo com tração nas quatro rodas possa descer com rapidez constante?

(Cap 5 – Ex 57) Um bloco de desliza sobre o topo de um bloco de . O bloco de tem uma aceleração de enquanto uma força horizontal de é aplicada a ele, como mostra a figura abaixo. Não existe atrito entre o bloco de e a superfície horizontal, mas existe atrito entre os dois blocos.

(a) Encontre o coeficiente de atrito cinético entre os blocos.

(b) Encontre a aceleração do bloco de durante o tempo em que o bloco de permanece em contato com ele.

(Cap 5 – Ex 71) Seu time de engenheiros de teste está prestes a soltar o freio de estacionamento de um carro de , de forma que ele irá descer por uma inclinação muito longa de em preparação para uma batida no fim da rampa. (Em uma inclinação de , a mudança na altitude é da distância horizontal viajada.) A força resistiva total (arrasto do ar e atrito de rolamento) para esse carro foi estabelecida previamente como , onde é a rapidez do carro. Qual é a rapidez terminal para o carro descendo por essa inclinação?

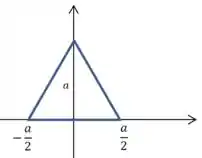
(Cap 5 – Ex 104) Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento . O triângulo tem um vértice no eixo e os outros em e .

(Cap 5 – Ex 63) Um bloco de de massa repousa na superfície inclinada de uma cunha de de massa, como na figura. Uma força horizontal é aplicada sobre a cunha, que desliza sobre uma superfície sem atrito.

(a) Se o coeficiente de atrito estático entre a cunha e o bloco é e a cunha tem uma inclinação de com a horizontal, encontre os valores máximo e mínimo da força para os quais o bloco não escorrega.

(b) Repita a parte (a) com .

(Cap 5 – Ex 66) (a) Um bloco está deslizando para baixo em um plano inclinado. O coeficiente de atrito cinético entre o bloco e o plano é . Mostre que o gráfico de em função de (onde é a aceleração ao longo da descida e é o ângulo de inclinação do plano em relação à horizontal) seria uma linha reta com inclinação e intercepto . (b) Os dados a seguir mostram a aceleração de um bloco deslizando por um plano inclinado como uma função do ângulo de inclinação do plano com a horizontal.

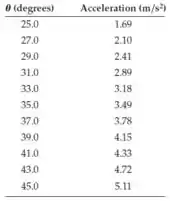
Usando um programa de planilhas, faça um gráfico desses dados e ajuste uma linha reta a eles para determinar e . Qual é a diferença percentual entre o valor obtido para e o valor usual de ?

(Cap 5 – Ex 97) Uma curva de raio é inclinada de forma que um carro de viajando a pode percorrê-la mesmo se a estrada está tão congelada que o coeficiente de atrito estático é aproximadamente zero. Você está compromissado a dizer à polícia local o intervalo de velocidades nas quais um carro pode viajar sobre essa curva sem derrapar. Negligencie os efeitos do arrasto do ar e do atrito de rolamento. Se o coeficiente de atrito estático entre a estrada e os pneus é , qual é o intervalo de velocidade que você entrega à polícia?

(Cap 5 – Ex 83) Você está girando sua irmã mais nova em um círculo de raio , como mostrado na figura. Se a massa dela é e você faz com que ela complete uma revolução a cada , (a) qual é a magnitude e a direção da força que deve ser exercida por você sobre ela? (b) Qual é a magnitude e a direção da força que ela exerce sobre você?

(Cap 5 – Ex 132) Um bloco de massa está sobre uma mesa horizontal. O bloco está preso a um bloco de ( através de um fio leve que passa por uma polia, sem massa e sem atrito, na beirada da mesa. O bloco de massa balança a do chão (Figura abaixo), O sistema é largado do repouso em e o bloco de atinge o chão em , O sistema é, agora, recolocado em sua configuração inicial e um bloco de é colocado sobre o bloco de massa Largado do repouso, o bloco de agora atinge o chão após . Determine a massa e o coeficiente de atrito cinético entre o bloco de massa e a mesa.